日本応用数理学会
2020年 年会
プログラム
2020年8月18日
9月8日
9月9日
9月10日
▷ 総合講演 [9月9日:15:10-16:30:A]
- 感染症数理モデルと COVID-19 / ○稲葉 寿 (東京大学大学院数理科学研究科) [概要]
感染症の数理モデルは1920年代末におけるケルマックとマッケンドリックの貢献から90年以上の歴史があり,80年代以降欧米では感染流行予測・制御の有力なツールとして発展してきたが,我が国での政策実装は大きく遅れ,今回のCOVID-19においてはじめて実践的に利用され,公的な議論の対象となった.本講演では,まず感染症数理モデルのキー概念である基本再生産数理論の最近の発展についてのべ,ついで,今回のCOVID-19が提起する感染症数理モデルの実践的適用に関する諸問題を考察したい.
▷ [研究部会OS] 幾何学的形状生成(1) [9月8日:09:10-10:30:A]
- 同一の crease と crease pattern をもつ「紙の曲線折り」について / ○梅原 雅顕 (東京工業大学・情報理工学院), 佐治 健太郎 (神戸大学・大学院理学研究科), 直川 耕祐 (広島工業大学・情報学部情報工学科), 本田 淳史 (横浜国立大学・大学院工学研究院), 山田 光太郎 (東京工業大学・理学院) [概要]
一般に与えられた「曲線折り」に対して,折り目の像としての空間曲線を crease とよび,折る前の紙に展開した状態での折り目に対応する平面曲線を crease pattern とよぶことにすると,与えられた 「曲線折り」は,局所的には,それと同じ crease とcrease pattern をもつ別の可能性がもう一つ存在することが以前から知られていた.本研究では,もう二つの新たな可能性があり,元のものと併せて,これら4個の「曲線折り」は,3次元Euclid空間の中で,一般に全部非合同となる,という結果を得た.応用として,空間閉曲線に沿った「閉曲線折り」の場合には,同じ crease とcrease pattern をもち,互いに非合同なものが無数に存在することも報告する.
- Rulingの配置を考慮した三角形分割による曲線折りの近似形状生成 / ○佐々木 好祐 (筑波大学), 三谷 純 (筑波大学) [概要]
曲線に沿って紙のような薄いシートを折ることで曲面を含む形状を生成できる。本発表では、実際に紙を曲線に沿って折ることで得られる形に近い形状をコンピュータで近似的に再現する手法を説明する。提案手法では、曲線に沿って折ったあとにできる形状のRulingの配置を推測し、これを利用する。この手法は、これまでの同様の目的を持った手法に比べて簡単かつに幅広い折り線のパターンに対応できる点で優れている。
- rulingを考慮しない四角形メッシュ分割を用いた曲線折りを含む可展面モデル生成 / ○野川 成己 (筑波大学システム情報工学研究科), 三谷 純 (筑波大学システム情報系) [概要]
線織面に属する可展面はrulingと呼ばれる直線要素から成る曲面であり、rulingを辺に含む四角形メッシュによって離散化表現することが多い。一方でDiscrete Orthogonal Netと呼ばれるrulingを用いない四角形メッシュモデルの有用性が報告されている。本発表ではこれを参考に、曲線を含む展開図を四角形メッシュ分割し、Origami Simulatorでシミュレートした結果を報告する。
- 三角形のねじり折りを用いたホール問題の解法 / ○山本 陽平 (筑波大学 情報システム研究科), 中里 陸 (筑波大学 情報システム研究科), 三谷 純 (筑波大学 情報システム系) [概要]
折り紙設計において,平坦折り可能な複数の展開図の接続を試みると展開図の間に隙間が生じる場合がある.その隙間を埋めるように折り線を配置する問題をホール問題と呼ぶ.本研究では,隙間の縁に接する折り線が,その縁に垂直となる場合に限定し,三角形のねじり折りを用いたホール問題の解法を示す.また,三角形のねじり折りを変形することで,解は無数に存在することを示す.
▷ [正会員OS] 乱数生成と評価 [9月8日:09:10-10:30:B]
- NIST SP800-22 におけるいくつかの検定間の関係に関する考察 / ○岩崎 淳 (京都大学) [概要]
NIST SP800-22乱数検定ツールに含まれる検定間の関係は部分的にしか解明されていない.本発表ではそれらのうちSerial1検定とSerial2検定の関係,および,頻度検定と累積和検定F,累積和検定Bの関係について考察する.前者の関係についてはp値の結合分布が導出される.後者については,うち2つの検定の結果から残り1つの結果を一定の確率で予測可能なことを示す.
- P値の厳密分布が一様分布と異なる場合のKolmogorov-Smirnov検定を用いた乱数性の判定について / ○山口 明宏 (福岡工業大学), 斉藤 朝輝 (公立はこだて未来大学) [概要]
乱数検定における乱数性の判定指標の一つとして,検定で得られたP値の分布と一様分布との適合度検定が用いられているが,乱数検定によってはP値の厳密分布が一様分布と異なることが知られている. 本研究では,カオス真軌道を用いて生成した理想的な乱数と統計的に同等な擬似乱数系列を用いて生成したP値の経験分布を参照分布として用いるKolmogorov-Smirnov検定を提案し,参照分布として一様分布を用いる場合,および,P値の厳密分布を用いる場合について比較した結果を報告する.更に,帰無仮説の分布と真の分布が異なる場合に,K-S検定統計量の期待値の上界を与える不等式を導出し,数値実験によって検証した結果も合わせて報告する.なお,前者の内容については,中止となった2020年研究部会連合発表会で講演予定だったものである.
- 量子コンピュータの解析手法としての乱数検定の可能性 / ○田村 賢太郎 (慶應義塾大学大学院理工学研究科), 鹿野 豊 (慶應義塾大学量子コンピューティングセンター, チャップマン大学量子科学研究所), ルディー レイモンド (慶應義塾大学量子コンピューティングセンター, IBM 東京基礎研究所) [概要]
NIST SP 800-22をはじめとした乱数検定は, 量子コンピュータの簡易的な診断に応用できる可能性がある. 量子コンピュータにとって乱数生成は本質的かつ基本的な働きであり, 出力乱数の検定を通して量子コンピュータの状態が解析できると考えられるためである. 本発表では乱数検定が量子コンピュータの診断に利用できる可能性の一端として, 実際の量子コンピュータの量子ビットにおける相互相関を出力乱数から解析した結果を示す.
- 2k-1次のエルミート多項式の置換多項式性とその乱数生成への応用 / ○梅野 健 (京都大学大学院情報学研究科) [概要]
2k-1次のエルミート多項式H_{2k-1}(x)を2^kで割った整数係数多項式(P_{2k-1}(x)と定義する)が2冪剰余環上で置換多項式であることを証明した。ここでkは任意の自然数である。
これはエルミート多項式の新しい性質であり、エルミート多項式の擬似乱数生成への応用が期待される。また、他の古典直交多項式である奇数次チェビシェフ多項式にも同様の
置換多項式性があることが講演者によって証明されていることから、偶然の一致ではなく、古典直交多項式(アナログの世界)と置換多項式(デジタルの世界)とが何がしかの関係
を有することが示唆される。
P_{2k-1}(x)の具体例:
P_1(x)=x, P_3(x)=2x^3-3x, P_5(x)=4x^5-20x^3+15x, P_7(x)=8x^7-84x^5+210x^3-105x, P_9(x)=16x^9-288x^7+1512x^5-2520x^3+945x, ….
参考文献 K. Umeno, “Key Exchange by Chebyshev Polynomials modulo 2^w”, Proc. INA-CISC (2005)
▷ [研究部会OS] 科学技術計算と数値解析(1) [9月8日:09:10-10:30:C]
- クロマトグラフィーモデルの直交選点有限要素法(OCFEM)による定式化と数値計算 / ○大久保 孝樹 (函館高専) [概要]
カラムクロマトグラフィーは、分析および薬剤や食品物質の精製分離に応用されている。本研究では、Langmuirの等温吸着式を用いたLDF(線形駆動力)モデルと1次元移流拡散反応方程式の連立偏微分方程式をOCFEMによる微分作用素行列によって時間および空間に関して離散化した。パラメーターを無次元化した連立偏微分方程式をOCFEMによって数値計算することによって、濃度分布に与える無次元パラメーターの影響を調べた。
- 異方的三角形分割上でももロバストな不連続 Galerkin スキーム / 柏原 崇人 (東京大学), ○土屋 卓也 (愛媛大学) [概要]
Galerkin有限要素法を一般化した不連続 Galerkin法(以下 DG 法とする)の誤差解析を行う際には、用いる三角形分割について形状正則性を仮定するのが通常である。この講演では、ペナルティー項の定義を変更することにより新たなDGスキームを定義し、三角形分割の形状正則性を仮定せずに誤差解析を行う。さらに数値実験により、提案されたDG法が異方的三角形分割上でロバストであることを確かめる。
- Diracのデルタ関数を含む3次元境界値問題に対する高精度な有限要素解析 / ○中野 泰河 (新潟大学大学院 自然科学研究科), 劉 雪峰 (新潟大学大学院 自然科学研究科) [概要]
本講演では,Diracのデルタ関数を含む3次元境界値問題の有限要素解析において,非一様メッシュと特異基底関数を組み合わせた解析手法を紹介する.
- Stokes 問題の圧力に Hermite 要素を用いる安定化有限要素法 / ○内海 晋弥 (学習院大学理学部) [概要]
Stokes 方程式に対する有限要素法を考える.粘性係数が小さい場合,広く使われているP2/P1要素近似より,P2/P2安定化法が有限要素解の精度が良いことが分かっている.しかし,離散化により導かれる連立一次方程式を反復法で解く際,後者の反復回数が多くなることが観察されていた.本報告で,圧力に Hermite 2次要素を使い安定化項を加える手法を提案する.小さい粘性係数問題に対する精度はP2/P2安定化法と同等で,反復回数はP2/P1要素と同等であることが観察される.
▷ [正会員OS] 先進的環境における数値計算と関連HPC技術(1) [9月8日:09:10-10:30:D]
- HPL-AI行列の観察とベンチマークプログラムの実装について / ○工藤 周平 (理化学研究所), 似鳥 啓吾 (理化学研究所), 今村 俊幸 (理化学研究所), 伊奈 拓也 (理化学研究所) [概要]
HPL-AIは新しいスーパーコンピューター向けのベンチマークであり,LINPACKベンチマークと類似しているが,混合精度演算を許可している点が最大の違いである.本発表では,HPL-AIにおいて変更された行列の定義を検証し,数値的問題点やそれを解消するための手法を示す.
- Parareal法における低精度演算・混合精度演算の活用 / ○大島 聡史 (名古屋大学), 飯塚 幹夫 (九州大学), 小野 謙二 (九州大学) [概要]
プロセッサの演算性能の向上が難しくなっている今日、現在主流である倍精度浮動小数点演算よりも低い精度の演算の活用が注目されている。本研究では、計算順序に依存性のある計算を並列に計算し、あとから補正計算を行って正しい解を得る時間並列計算法の一種であるParareal法を対象として、低精度演算・混合精度演算の適用について行った検討や実験の結果を発表する。
- 自動チューニング言語ppOpen-ATによる混合精度演算の最適化機能について / ○片桐 孝洋 (名古屋大学 情報基盤センター), 山梨 祥平 (名古屋大学 大学院情報学研究科), 八代 尚 (国立環境研究所 地球環境研究センター), 大島 聡史 (名古屋大学 情報基盤センター), 永井 亨 (名古屋大学 情報基盤センター) [概要]
本発表では、自動チューニング機能を任意のプログラムに自動付加する計算機言語ppOpen-ATの新機能について説明する。本新機能は、プログラム上において混合精度演算をする箇所を指定することで、演算精度を考慮して最速となる実装方式を自動選択する。性能評価を、名古屋大学情報基盤センターに設置され2020年7月1日から正式運用開始したスーパーコンピュータ「不老」TypeⅠサブシステム(スーパーコンピュータ「富岳」型ノード)を用いて行った結果を紹介する。
- FPGAクラスタによるカスタム高性能計算の現状と課題 / ○佐野 健太郎 (理化学研究所) [概要]
理化学研究所では、現在、複数のFPGAを専用ネットワークで相互接続したFPGAクラスタシステムを研究開発している。本システムでは、ユーザが問題に特化したカスタム計算回路をプログラムすることにより、回路再構成可能なFPGAの特徴を生かしたカスタム高性能計算を行うことができる。システムの概要やプログラミング方法に関する現状を紹介すると共に、性能最適化などの課題について講演する。
▷ [研究部会OS] 数論アルゴリズムとその応用(1) [9月8日:09:10-10:30:E]
- 同種写像暗号OSIDHの理論的背景について / ○小貫 啓史 (東京大学) [概要]
向き付けられた楕円曲線とは、楕円曲線とその自己準同型間への虚二次体の整環の埋め込みのペアのことである。2019年、ColoとKohelは、同じ整環により向き付けられ楕円曲線の同値類の集合がその整環のイデアル類群の単純推移作用を持つと述べ、それに基づく鍵共有方式OSIDHを提案した。本講演では、彼らが証明なしに述べた上記の主張には若干の修正が必要であることを示す。また、OSIDHがうまく動かないパラメータが存在することを示し、そのようなパラメータを避けるための十分条件を提示する。
- 同種写像による点の像の判定困難性に基づく公開鍵暗号方式 / ○守谷 共起 (東京大学大学院情報理工学系研究科 博士1年), 小貫 啓史 (東京大学大学院情報理工学系研究科 特任研究員), 高木 剛 (東京大学大学院情報理工学系研究科 教授) [概要]
超特異楕円曲線間の同種写像を求める計算問題に安全性の根拠を持つ同種写像暗号は,量子計算機に耐性のある暗号として期待されている.SIDHやCSIDHといった同種写像暗号の基本的な方式では,いずれも超特異楕円曲線を共有鍵として生成するため,超特異性判定を用いることで選択平文攻撃に対して判別可能となる(IND-CPA安全ではない).本講演では,これらの方式にsmoothな位数を持つ点を付加することにより,IND-CPA安全な暗号方式となるSiGamalとC-SiGamalを提案する.本暗号方式は,秘密鍵である同種写像による像を計算し,smoothな位数を持つ点の離散対数問題を解くことをトラップドアとしている.IND-CPA安全性は,ある楕円曲線上の与えられた点が隠された同種写像による像であるかの判定問題の困難性に帰着される.
- Kohel-Lauter-Petit-Tignolアルゴリズムのsageにおける実装報告 / ○神戸 祐太 (埼玉大学), 安田 雅哉 (立教大学), 横山 和弘 (立教大学) [概要]
有限体上の超特異楕円曲線の自己準同型環と四元数環のmaximal orderの間にはDeuring対応と呼ばれる1対1対応がある. Kohel-Lauter-Petit-Tignol(KLPT)アルゴリズムは,与えられたmaximal orderを持つ超特異楕円曲線を見つけるconstructive Deuring対応問題を解くツールで暗号分野で幅広い応用先を持つ. しかし,KLPTアルゴリズムの実装に関する文献は少なく,10ビット程度までの標数における実装報告しかない. 本発表ではKLPTアルゴリズムの改良を行うと共に45ビット程度までの標数におけるsageによる実装結果を報告する.
- Efficient algorithms for finding and enumerating superspecial Howe curves in much larger characteristic / ○工藤 桃成 (東京大学), 原下 秀士 (横浜国立大学), Howe Everett [概要]
超特別曲線は超特異曲線の中でも有限個しかない曲線クラスであり,その存在性の決定と数え上げは基本的かつ重要な問題である.これまで講演者は種数4,5の場合に上記問題を解くための様々なアルゴリズムを提案し,小さい標数p(最大でもp=23)に対し上記問題を解決してきた.一方で近年,千田氏は種数4の曲線の中でも超特別となる可能性の高いHowe曲線に着目し,上記問題を解くアルリズムを提案しMagmaに実装した(JANT2019春の発表).しかしその計算量は最悪O~(p^9)であり,実際,p<100程度までしか計算結果は得られていなかった.
そこで今回,超特別Howe曲線を決定する新たなアルゴリズムとして,千田氏によるものを改良した方式と,Richelot同種写像の計算に基づく方式の二つを提案する.前者はO~(p^6),後者はO~(p^4)の計算量であり,後者をMagma上で実行することで全てのp7に対する超特別Howe曲線の存在性予想を提示する.
▷ [一般講演] 一般講演(1) [9月8日:09:10-10:30:F]
- 積型DNNの表現能力とパーセプトロンによる設計 / ○長瀬 准平 (芝浦工業大学大学院/ZOZO研究所), 斎藤 侑輝 (ZOZO研究所), 中村 拓磨 (ZOZO研究所), 石渡 哲哉 (芝浦工業大学) [概要]
現代の様々な分野で多くのDNNが提案・活用されている.一方で,その体系的な理論の整備は未だ行われていないのが現状である.本研究では,近年注目を集める構造の一つであるアテンションについて着目し,有限の表現能力の議論を行う.結果として,単純なDNNであるパーセプトロンによって特徴量間のインタラクションを等価に表現できることを数学的に示し,それらモデルの統一化およびモデル構造の体系化を試みる.
- 常微分方程式モデルの学習における離散化手法の影響について / ○寺川 峻平 (神戸大学大学院システム情報学研究科), 松原 崇 (大阪大学大学院基礎工学研究科), 谷口 隆晴 (神戸大学大学院システム情報学研究科) [概要]
近年,データから微分方程式モデルを学習する試みが行われているが,データを完全に再現できたとしても,得られるモデルには学習時に用いる離散化手法に依存したモデル化誤差が生じる.本研究では,テスト方程式を一般のRunge-Kutta法を用いて学習した場合におけるモデル化誤差を解析する.また,いくつかの手法について,実際にニューラル常微分方程式による学習を行い,その結果を解析結果と比較する.
- 分布系のカオス同期化とニューラルネットワークを用いた秘匿通信システム / ○陳 鈺涵 (神戸大学大学院システム情報学研究科), 佐野 英樹 (神戸大学大学院システム情報学研究科), 若生 将史 (神戸大学大学院システム情報学研究科), 谷口 隆晴 (神戸大学大学院システム情報学研究科) [概要]
本発表では,偏微分方程式のカオス同期化とニューラルネットワークを用いた秘匿通信システムを提案する.先行研究では,ある非線形な境界条件に由来する,波動方程式のカオス振動を利用した手法が提案されていたが,境界条件を表す数式は,比較的,簡素なものであり,情報の漏洩の可能性がある.本研究では,これをニューラルネットワークを用いて近似することでブラックボックス化し,より情報が漏洩しにくい方式に改良する.
▷ [研究部会OS] 幾何学的形状生成(2) [9月8日:10:40-12:00:A]
- Spherical Kaleidocycles on 3-sphere / ○Park Hyeongki (Kyushu University), Jakub Rondomanski (Free University of Berlin), Kenji Kajiwara (IMI, Kyushu University), Polthier Konrad (Free University of Berlin) [概要]
We consider rings of equivalent geodesic tetrahedra on 3-sphere, which is called the spherical Kaleidocycles. For the global rotation in the particular direction of spherical Kaleidocycles exhibits “turning over” motion via the stereographic projection. We present an algorithm to construct spherical Kaleidocycles and realize them by the Javaview.
- 剛体折紙の折線パターンの最適化と近似曲面形状生成法 / ○早川 健太郎 (京都大学), 大崎 純 (京都大学) [概要]
剛体折紙は面を変形させることなく折ることのできる折紙であり,さまざまな工学的応用が存在する。本研究では,目標曲面を近似する平面展開可能かつ剛体折り可能な多面体形状を最適化手法と部分剛接合骨組の力学特性を用いて生成する。提案手法を用いることで,ミウラ折りなどの典型的な折線パターンに依存することなく,さまざまな変形自由度をもつ剛体折紙機構を得ることができる。
- 曲線折りを有する仮設建築物の提案,―剛体変位による形状決定法と剛性評価― / ○有村 崇 (鹿児島大学 理工学研究科 工学専攻 建築プログラム 修士1年) [概要]
本研究では、近年需要の増す仮設住宅に対して折り紙の曲線折りという手法を取り入れ、可搬性と構造強度の充実を実現することを目的とし、建築分野で用いられてきた一般逆行列による剛体変位を折り紙の剛体折りと曲線折りに適用する。本発表では、剛体折りや曲線折り等の折り紙の理論について触れ、提案する曲線折りを有する仮設建築物のモデルや剛体変位の式による形状決定法について解説し、これらの数値結果を示す。そして解析モデルや境界条件、外力条件などの各種条件設定による解形状の違いを示す。
- 平面弾性曲線の等周変形の楕円テータ関数による明示公式の構成 / ○重富 尚太 (九州大学大学院数理学府), 梶原 健司 (九州大学マス・フォア・インダストリ研究所) [概要]
オイラーの弾性曲線と呼ばれる、一次元弾性体を曲げたときに現れる曲線の、弧長を一定に保つような変形を表す明示公式を、楕円テータ関数が満たす恒等式を用いて構成する。連続曲線を連続的に変形するもの、離散曲線を連続的に変形するもの、離散曲線を離散的に変形するものの三つを紹介する。
▷ [研究部会OS] 応用カオス(1) [9月8日:10:40-12:00:B]
- 超一般化Boole変換における無限エルゴード性とMittag-Leffler分布 / ○大久保 健一 (大阪大学), 梅野 健 (京都大学) [概要]
無限測度を保存する力学系では, エルゴード的であっても, 時間平均と相平均が一致しない現象が生じる. 本講演では超一般化Boole変換においてパラメータがα=±1の場合に, Lebesgue測度を保存し, エルゴード的であることの証明を述べ, normalized Lyapunov exponentがオーダー1/2のMittag-Leffler分布に従うことを示す.
- ハミルトニアン系カオスに対する拡張型カオス尺度について / ○井上 啓 (山陽小野田市立山口東京理科大学工学部), 真尾 朋行 (東芝情報システム株式会社・京都大学大学院情報学研究科), 奥富 秀俊 (東芝情報システム株式会社), 梅野 健 (京都大学大学院情報学研究科) [概要]
ハミルトニアン系カオスを拡張型カオス尺度により定量化することを試みる。具体的には、ハミルトニアン系カオスを示す保存系のモデルである標準写像を取り上げ、その拡張型カオス尺度の計算を行う。適切な初期値を選べば同モデルによる軌道はカオスを示すことが知られている。また、保存系であるため、リアプノフ指数の合計が常に0となる。そのため、標準写像の拡張型カオス尺度の値が0となるかどうかについて比較検討を行う。
- 可解カオスのj-不変量による分類について / ○梅野 健 (京都大学大学院情報学研究科) [概要]
登壇者の発表論文[1]で発表した可解カオス系は楕円関数の母数が
実数である楕円関数を対象とするものであったが、本研究は、楕円関数の母数が複素数に対応するものに拡張しても(上記の文献の、l,とmという2つのパラーメーターを互いに
複素共役にしても実可解カオス解があることをまず示す。この場合、2つのパラメーターがあるということで複素母数の楕円関数解が初めて構成できる。
その上で、その楕円関数解から、その可解カオスのj-不変量を求める。するとこのj-不変量は可解カオスのパラメーターで簡潔に書け、
このj-不変量の整数性などの性質から虚数乗法を持つ楕円関数の加法公式で与えられる可解カオス系と虚数乗法を持たない楕円関数のクラスで与えられる可解カオス系の分類
を行うことができ、虚数乗法を持つ楕円関数の加法公式で与えられる可解カオスのリストアップ(有限個)を行うことができる。これらの可解カオスの新たな展開について
得られた成果を発表する。
[1] K. Umeno, “Method of constructing exactly solvable chaos”, Phys. Rev. E(1997) Vol. 55, pp.5280-5284.
- 任意のべき指数α<2の安定分布はβ=±1の2つの完全非対称安定分布の和へ分解できる-超一般化中心極限定理の逆について- / ○梅野 健 (京都大学大学院情報学研究科) [概要]
任意のべき指数α<2の安定分布はβ=±1の2つの完全非対称安定分布の和へ分解できることを証明した。
これは、任意のべき指数(α<2)、β(歪度), スケールパラメーターγ*を与えた時に、常に、分布1 (べき指数α,β=1, スケールパラメーターγ_{1})と分布2(べき指数α,β=-1,スケールパラメーターγ_{2})の
2つの分布を確率p及1-pで独立に発生した確率過程と捉えることができることになる。但し、確率pとβとは1対1の関係でユニークに定まる。
これは、以前証明した超一般化中心極限定理の逆に相当するものであり、α<2の安定分布の範囲で分解は一意に定まる。また反対に(α=2)のガウス分布の時には、非対称安定分布が定まらない
ことになる。これらの結果は、安定分布の混合分布を考える、あるいは時系列解析での逆問題(時系列から安定分布を推定)を考える上で参考になるものと考えられる。
▷ [研究部会OS] 科学技術計算と数値解析(2) [9月8日:10:40-12:00:C]
- 境界値問題の近似解の各点誤差評価 / ○劉 雪峰 (新潟大学) [概要]
本研究では、偏微分方程式の境界値問題に対して、1950年代に現れた加藤・藤田の手法と有限要素法との組み合わせによって、領域の内部の点における方程式の解の関数値を厳密に算出手法を提案します。最大値ノルムの誤差評価により、領域の内部の点における解の近似値の高次誤差収束が得られています。一次適合有限要素法の場合、内部の点では関数値の2次誤差収束(O(h^2))が可能となっています。
- IMT型DE公式による第2種Fredholm積分方程式の数値解法 / ○緒方 秀教 (電気通信大学) [概要]
本講演では,1次元第2種Fredholm積分方程式に対するDE公式による数値解法の改良として,IMT型DE公式による解法を提案する.DE公式による解法は分点数に対し台形則のメッシュ幅をどう選ぶかが自明にわからないが,IMT型DE公式に公式を用いた場合はそのような問題は起こらない.しかも,近似解の精度はDE公式を用いた場合と同程度の高精度であることが,数値実験により示される.
- 片側急減衰関数の全無限積分に対する二重指数関数型数値積分公式 / ○岡山 友昭 (広島市立大学情報科学研究科) [概要]
様々なケースの積分に対し,被積分関数が遠方で二重指数関数的に減衰するように変数変換を行った上で,打ち切った複合台形則を適用する方法が提案されており,総称して二重指数関数型数値積分公式(略してDE公式)と呼ばれる.ただし,x→∞では指数関数的に減衰するが,x→-∞では多項式的に減衰するような片側急減衰関数の全無限積分に対しては,これまでDE公式が提案されていない.そこで本研究では,片側急減衰関数の全無限積分に対しDE公式を提案する.
- Numerical reconstruction of the spatial component in the source term of a time-fractional diffusion equation / Jiang Daijun (Central China Normal University), ○劉 逸侃 (北海道大学電子科学研究所), Wang Dongling (Northwest University (China)) [概要]
This talk is concerned with the analysis on the numerical reconstruction of the spatial component in the source term of a time-fractional diffusion equation. This ill-posed problem is solved through a stabilized nonlinear minimization system by an appropriately selected Tikhonov regularization. The existence and the stability of the optimization system are demonstrated. The nonlinear optimization problem is approximated by a fully discrete scheme, whose convergence is established by a newly-established uniform H^1 estimate of the solution to the discrete forward system. The iterative thresholding algorithm is proposed to solve the discrete minimization, and several numerical experiments are presented to show the efficiency and the accuracy of the algorithm.
▷ [正会員OS] 先進的環境における数値計算と関連HPC技術(2) [9月8日:10:40-12:00:D]
- Intel Xeonプロセッサ上におけるAVX512を用いた倍々精度演算の性能評価 / ○土肥 樹 (工学院大学), 菱沼 利彰 (株式会社科学計算総合研究所), 田中 輝雄 (工学院大学), 藤井 昭宏 (工学院大学) [概要]
我々は高速な高精度反復解法の実現を目的として,倍精度変数4つを同時演算できるSIMD拡張命令AVX2を用いて高精度演算の実装手法のひとつである倍々精度演算を高速化してきた.
近年,Intel Xeonプロセッサ上で倍精度変数8つを同時演算できるSIMD拡張命令AVX512が登場した.本研究ではAVX512を用いて反復解法で多くの時間を占める倍々精度ベクトル演算とCRS形式の倍精度疎行列と倍々精度ベクトルの積を高速化し,SIMD化による性能向上率をもとに評価した.
- Intel AVX-512IFMA命令を用いた複数のMontgomery 乗算の高速化 / ○高橋 大介 (筑波大学) [概要]
本論文では,Intel AVX-512IFMA命令を用いて複数のMontgomery乗算を高速化し,性能評価を行った結果について述べる.
提案した実装は,修正Montgomery乗算アルゴリズムに基づいている.
52ビット以下のMontgomery乗算オペランドに対して,Intel AVX-512IFMA命令を用いた実装は,Intel 64およびIntel AVX-512F命令を用いた実装に比べて高速に複数のMontgomery乗算が行えることを示す.
- 不均一なコア割付による動的負荷分散手法の検討 / ○河合 直聡 (東京大学 情報基盤センター), 伊田 明弘 (東京大学 情報基盤センター), 中島 研吾 (東京大学 情報基盤センター) [概要]
近年ではアプリケーション毎に様々な並列化手法が研究、開発されているが、システムの大規模化に伴い、均一な負荷分散が難しくなってきている。
本研究ではプロセス毎に割り付けられるコア数(スレッド数)をコントロールし、コア毎の負荷を均一にする手法について検討する。
手法の効果は、低ランク構造行列法に適用して確かめる。
- メニィコアクラスタ向け並列多重格子法 / ○中島 研吾 (東京大学情報基盤センター) [概要]
並列多重格子法は,エクサスケールシステムにおける大規模問題向け数値解法として注目されている。本研究では,並列多重格子法のメニィコアクラスタにおけるノード内性能の最適化に注目し,実装例とOakforest-PACS(JCAHPC),Fujitsu PRIMEHPC FX700を使用した性能評価事例を紹介する。
▷ [研究部会OS] 数論アルゴリズムとその応用(2) [9月8日:10:40-12:00:E]
- Diene-Thabet-Yusuf の3次多変数署名方式の安全性について / ○橋本 康史 (琉球大学) [概要]
有限体上の非線形多変数多項式の集合を公開鍵とする公開鍵暗号を多変数多項式暗号とよぶが、その多くは2次多項式で構成される。ごく最近, Diene-Thabet-Yusuf は3次多項式で多変数署名方式を構成した。この方式では、3次化する方法を工夫することで、それほど効率性を落とさずにすんでいるが、一方でその工夫は安全性を損なっている。本講演では、この署名方式の構成とその脆弱性について話をする。
▷ [研究部会OS] ウェーブレット [9月8日:10:40-12:00:F]
- ウェーブレット・パケットのグラフ上での自然な構成について 【OS企画講演 60分】 / クロニンジャー アレクサンダー (カリフォニア大学サンディエゴ校数学科), 李 昊天 (カリフォニア大学デイヴィス校数学科), ○斎藤 直樹 (カリフォニア大学デイヴィス校数学科) [概要]
グラフ上での信号処理では, グラフ・ラプラシアンの固有値と固有ベクトルを, 通常の信号処理における周波数と余弦・正弦関数と見做すことが多いが, この見方が厳密に正しいのは, パスやサイクルといった単純なグラフ上だけである. そこで, グラフの「双対空間」の構成, その上での「Littlewood-Paley理論」の展開により, グラフ・ウェーブレット・パケット変換を構築する方法を提案する.
▷ [研究部会OS] 幾何学的形状生成(3) [9月8日:13:20-14:40:A]
- カーネル法を用いたデータ点からの曲面の生成法 / ○寒野 善博 (東京大学) [概要]
計算力学におけるデータ駆動型の手法の展開の一つに,通常の材料構成則に代えて材料実験で得られたデータをより直接的に数値シミュレーションに用いるという方法論がある.実験データとして応力・ひずみ空間におけるいくつかの点が得られたとき,これらの点は通常はある曲面の上にあると考えられる.この曲面を推定するノンパラメトリックな手法として,本研究では,カーネル法に基づく手法を提案する.
- グラフ曲面による形状表現を用いた連続体シェルの釣合い形状設計法 / ○堺 雄亮 (京都大学大学院工学研究科建築学専攻), 大崎 純 (京都大学大学院工学研究科建築学専攻) [概要]
本研究では,グラフ曲面として記述された連続体シェルの釣合い形状を,有限差分法を用いて陽的な反復解法で求める手法を提案する.本手法では,水平応力成分をPucher’s formulationのパラメータとして与えるため,設計者の望む応力分布を有する曲面を生成できる.さらに,解析対象領域内部に境界を有する曲面,せん断項を非零とした複雑な曲面形状の設計が容易に行える.数値例題で,釣合い解および支点反力の鉛直成分により解の妥当性を示す.
- Kirchhoffシェル要素を用いた初期曲げによる木質シェル構造の形状最適化 / ○貞廣 渉 (鹿児島大学大学院理工学研究科工学専攻建築プログラム横須賀研究室) [概要]
平坦な四辺形パネルで構成されるPQ meshは、接合部が単純化され、部材に対する曲げ加工が不要であり、生産性、施工性等に優れた曲面表現手法である。本研究ではKirchhoffシェル要素を用いた平板要素に対し、初期曲げを作用させることで、PQ meshにより構成された自由曲面形状の生成を行っている。初期形状、初期曲げの変化や、生成された形状に対する線形結合により、多様な形状を生成し形状最適化を行う。
- 測地線による木質グリッドシェル構造の幾何学的非線形解析 -NR法による釣合い経路の追跡- / ○中島 尚哉 (鹿児島大学大学院理工学研究科工学専攻建築学PG 横須賀研究室) [概要]
測地線を用いた曲線材は、通直な板材を設計形状に従い曲げ加工を行うことで任意の曲面形状を構成することができる。既往の研究では測地線グリッドシェルの力学性状の評価や構造最適化による優位性は線形解析を用いた構造解析によって検証しているが、座屈挙動を把握する非線形解析は行われていない。本研究では測地線グリッドシェルの幾何学的非線形解析を行い、測地線とは異なるモデルと結果を比較し、力学性状の評価を行う。
▷ [研究部会OS] 応用カオス(2) [9月8日:13:20-14:40:B]
- 時系列データ予測における Time Scaling Regression Method の提案とその性能評価 / ○新谷 健 (京都大学大学院情報学研究科、フォルシア株式会社), 梅野 健 (京都大学大学院情報学研究科) [概要]
時刻t → 0 が未来の方向を表す減衰的指数関数に従う時系列データにおいて、指数関数の対数を考えて予測する方法だと、時刻t → 0 において大きな差を生む予測となる。
この問題を解決するために、値域をlogでスケーリングするのではなく、時刻の領域をスケーリングする time scaling regression method を提案する。
また、この方法の導入により、予測精度が向上することを確かめる。
- 地震の時間間隔における階層構造の特徴と確率予測への応用 / ○田中 宏樹 (京都大学), 梅野 健 (京都大学) [概要]
マグニチュードを重みとした地震の点過程における時間間隔について, その階層構造を特徴づける方法と, 地震カタログを解析して見出された性質について述べる. その応用として, 小さいマグニチュードの地震の情報を用いて大きい地震の発生時刻を確率予測する方法を提案し, 地震の時系列をよく再現する確率モデルを用いて構成した人工カタログに適用した結果について議論する.
- Reward-modulated Hebbian Learningを用いたエージェントの行動学習とその内部情報表現 / ○中原 公彦 (福岡工業大学大学院工学研究科), 山口 裕 (福岡工業大学情報工学部) [概要]
リカレントネットワークのひとつであるレザバー計算ネットワークにより制御される移動ロボットエージェントに障害物回避タスクを与え,自律的な行動学習を行った.そして行動獲得時のネットワークの内部情報表現について分析した.学習はReward-modulated Hebbian Learningルールを用いて行った.その結果,障害物回避行動を獲得し,障害物との距離や運動についての内部情報表現が得られた.
- Neural ODEによる画像認識過程の可視化 / ○角田 千哉 (福岡工業大学大学院工学研究科), 山口 裕 (福岡工業大学情報工学部) [概要]
Neural ODEは微分方程式によって表現された,入力層から出力層まで連続的な変換を行うニューラルネットモデルである.本研究ではNeural ODEを用いた画像認識モデルを実装し,情報表現の変換過程の推移を可視化を行い,またダイナミクスとしての性質を調べた.
▷ [研究部会OS] 科学技術計算と数値解析(3) [9月8日:13:20-14:40:C]
- 非双曲型平衡点近傍でのLyapunov関数の数式処理・精度保証による構成 / ○新田 光輝 (電気通信大学), 笹木 俊希 (電気通信大学), 山本 野人 (電気通信大学) [概要]
連続力学系における非双曲型平衡点近傍では、局所的なLyapunov関数に対してでさえも一般的な構成法は存在しない。ここでは力学系の標準型理論を援用し、数式処理と精度保証を組み合わせることで、多項式で表される局所Lyapunov関数を半自動的に構成することを試みる。
- 離散力学系における不動点近傍での安定多様体の捕捉について / 皆本 啓吾 (電気通信大), 新田 光輝 (電気通信大), ○山本 野人 (電気通信大) [概要]
離散力学系の双曲型不動点近傍では、精度保証によるLyapunov関数の構成が可能であることが知られている。
本講演では、安定多様体の数値的な捕捉をLyapunov関数を利用した精度保証法で行う方法について考察する。
特に、サドル型不動点を扱い、安定多様体が連続に存在する範囲を精度保証で特定できることを示す。
また、高次元の問題に対する方法の展望も述べたい。
- 精度制御型複素積分と電子状態計算ソフトRSDFTへの応用 / ○小橋 恒士 (鳥取大学工学研究科), 吉見 一慶 (東京大学物性研究所), 田中 健一郎 (東京大学情報理工学系研究科), 星 健夫 (鳥取大学工学研究科) [概要]
グリーン関数を用いたスペクトル計算に対する,精度制御型計算を提案する.スペクトル計算は,電子状態計算などで大きな需要がある.通常は大行列固有値問題に帰着され,計算量の観点から困難になる.計算量のより軽い複素積分を帰着することができるが, 精度検証が必要となる.本研究では,スペクトル計算を複素積分に帰着し,積分値に対する誤差上界(エラーバー)を,台形公式に対する複素関数論的誤差評価を用いて陽に与え,必要精度を確保する.誤差上界の評価式および,大規模電子状態計算ソフトRSDFTを用いた数値例を示す.
- Second-order adjoint方程式に基づくヘッセ行列の計算について / 伊藤 伸一 (東京大学地震研究所), 松田 孟留 (理化学研究所脳神経科学研究センター), ○宮武 勇登 (大阪大学サイバーメディアセンター) [概要]
微分方程式の数値解を用いて定義された関数を最小化する問題は,データ同化など多くの文脈であらわれる.このような問題を解く際,目的関数の初期値に関する勾配やヘッセ行列の情報が必要になるが,陽に微分することは一般に困難である.近年,adjoint方程式を適切なRunge—Kutta (RK) 法で離散化すれば勾配を厳密に計算できることが示されている.本講演では, second-order adjoint方程式を適切なRK法で離散化することで,ヘッセ行列を厳密に計算できることを示す.
▷ [研究部会OS] 連続体力学の数理(1) [9月8日:13:20-14:40:D]
- 超音速すべり接触:解析解の導出と実験との比較 / ○山口 哲生 (九州大学), 家敷 拓弥 (九州大学), 澤江 義則 (九州大学) [概要]
2つの物体を接触させ,すべらせる接触形態のことをすべり接触という.本研究では,互いに平行な2つの円筒同士をすべり接触させたときに,すべり速度が物体の弾性波(S波速度)を上回る超音速条件において,変形の解析解をはじめて求めることに成功した.講演では,導出の詳細を報告し,実験結果との比較を議論する.
- 制約つき最適化問題として見たき裂進展モデル / ○高石 武史 (武蔵野大学工学部) [概要]
Bourdin-Francfort-Marigo により導入されたフェーズフィールドを用いた変分型のき裂進展モデルは,制約付きのエネルギー最小化問題としてスタートしており,木村氏と筆者の導出した時間発展モデルも同様に書き直すことができる.ここでは,き裂進展の時間発展方程式を制約つき最適化問題として書き直すことで問題の性質を見直すとともに,従来の時間発展モデルとして解いた結果と制約条件つき最適化として解いた結果を比較することで,比較的容易な時間発展型数値計算の結果の検証を行った.
- 静圧または全圧を含む境界条件を課した射影法の提案 / ○松井 一徳 (金沢大学大学院 自然科学研究科 数物科学専攻) [概要]
非圧縮性Navier-Stokes方程式に対する数値解法として射影法が知られている。本講演では、静圧または全圧を含む境界条件を課した射影法を提案し、その安定性と収束性について一般的な境界条件の場合のものと比較しつつ議論する。ここで、静圧は流体の圧力のことであり、全圧とは圧力と単位体積あたりの流体の運動エネルギーの和である。
- 膨張する円周解上のKuramoto-Sivashinsky方程式の差分解法について / ○小林 俊介 (京都大学理学研究科附属サイエンス連携探索センター), 矢崎 成俊 (明治大学理工学部) [概要]
Kuramoto-Sivashinsky方程式により定まる法線速度をもつ界面方程式は,厳密解として時間と共に拡がっていく円周解をもつ.この円周解近傍で定められた摂動が満たすべき偏微分方程式に対して,クランク・ニコルソンスキームによる差分近似を行い,近似解の存在・一意性・収束性について得られた結果を報告する.
▷ [一般講演] 一般講演(2) [9月8日:13:20-14:40:E]
- 前神経細胞の出現が上皮系の運動に及ぼす影響:数理モデルによる検討 / ○黒田 茂 (青森大学) [概要]
多細胞生物は上皮細胞シートのみからなる無神経生物から、上皮ー神経系からなる体制へと進化したと言われている。このような進化はなぜ・何の為に起こったのか?初期神経系の起源の問題に、個体における動く仕組みの進化の観点からアプローチした。実験的観察から着想を得て、上皮系、上皮ー神経系の数理モデリングを行い、埋め込み境界法を用いたシミュレーションを行った。本発表では、上皮系に当初突然変異的に現れたであろう少数の神経様細胞が及ぼし得る個体の動きへの影響とその生態学的意義(特に個体の移動能力に及ぼす影響)について報告する。
- 開放系化学反応ネットワークにおける散逸速度とエネルギー依存性 / ○小松 弘和 (京都大学 ウイルス・再生医科学研究所), 大岡 英史 (理化学研究所 環境資源科学研究センター), 中村 龍平 (理化学研究所 環境資源科学研究センター), 望月 敦史 (京都大学 ウイルス・再生医科学研究所) [概要]
本研究では,系外への流出が存在する円環状の化学反応ネットワーク(CRN)を対象とし,平衡状態への収束速度(散逸速度)が,制御可能なパラメータであるエネルギーの増加によってどのように振る舞うかを理論的に解明する.具体的には,このCRNの物質の濃度ダイナミクスを記述する常微分方程式の特性指数に着目し,そのエネルギーの増加に関する振る舞いを,ネットワーク構造から特定される反応のエネルギー依存性によって特徴づける.これにより,散逸速度はエネルギーの増加に関して,加速するだけでなく,減速,定速にもなりうることが示される.
- 医療画像診断への位相的データ解析の応用 / ○寺本 敬 (旭川医科大学医学部) [概要]
医療機器の発達と普及により、画像データの質と量は急速に増大している。
計量形態学等による客観的な分類基準を導入し、それを実現する系統的な診断の自動化によって、画像診断を支援したい。本研究では、位相的データ解析で開発された数学ツール(CHomP, DIPHA 等)を、医療画像データの定量的計測診断に適用する試みを、診断医らと進めてきた。骨 CT 3 次元画像のベッチ数指標、免疫染色化学画像のパーシステントホモロジーによる分類事例と、機械学習とを組み合わせる最近の発展について紹介する。
- ゲル基質上の上皮細胞シートが引き起こす浸透圧勾配依存的なドーム形成とその数理モデル / ○秋山 正和 (明治大学・先端数理科学インスティテュート), 石原(石田) すみれ (北海道大学・大学院先端生命科学研究院・細胞ダイナミクス科学研究室), 須志田 隆道 (サレジオ工業高等専門学校・情報工学科), 芳賀 永 (北海道大学・大学院先端生命科学研究院・細胞ダイナミクス科学研究室) [概要]
動物の複雑な体構造は,上皮組織の座屈や折れ曲がり,伸長といった単純な変形が積み重なることにより形成される.上皮組織が折れ曲がる変形のひとつにドーム状の形態形成があるが,そのような形態を引き起こす要因はほとんど分かっていない.そこで,ECM層と細胞層をカップルさせた数理モデルを構築し現象の再現を試みた.その結果,昨年度発表したモデルよりも更に簡単なモデルでも現象の再現が可能となった.
▷ [研究部会OS] 数理政治学 [9月8日:13:20-14:40:F]
- Arms Expansion and Transparency in Defense Policy / ○岩波 由香里 (大阪市立大学経済学研究科), 岡澤 亮介 (大阪市立大学経済学研究科) [概要]
We develop a career concern model to explore why some states expend tremendous resources on the national security and how transparency in defense policy influences the policy choice and the subsequent likelihood of deterrence success. In our model, the policymaker’s ability and the state of the world are unobserved to the citizens, but the citizens draw inferences about the policymaker’s ability from the policy outcome and the enacted policy if it is observable. The citizens’ evaluation influences the utility of the policymaker, which gives her incentives to appear competent. We demonstrate that when defense policy is not observable to the citizens, a low ability policymaker is inclined to enact the costly expansion policy to secure deterrence success and enhance her reputation. This leads to the overallocation of resources to national defense and the emergence of a possibly unnecessarily militarily strong state. However, we also find that transparency in defense policy may create perverse incentives and worsen the welfare of the citizens. Specifically, if the citizens initially believe that the country is likely to be in the safe state, the incompetent type may enact the costly policy to appear competent even though such a policy seems highly unnecessary. In other situations, transparency may render the policymaker’s reputational gain from the costly policy negative, discouraging her from enacting the costly policy even if the information she obtains suggests otherwise. In the former case, transparency is likely to trigger arms expansion, whereas in the latter, it is likely to cause deterrence failure.
- 複雑ネットワークにおけるランダムウォーカーの混雑についての考察 / ○田村 和広 (静岡大学) [概要]
本研究ではネットワーク上でランダムウォークする複数の粒子について考える。このようなネットワーク上のブラウン運動する粒子のモデルには既存のページランクという概念が存在する。しかし、多数の粒子を用いた場合においては単純なページランクでは粒子の混雑(鬱滞)を予測することが難しいことが示された。さらに、このようなモデルにおいて粒子の混雑を予測する既存および新たな中心性の知見を発見することができた。
- 議席配分問題における公平性についての考察 / ○諸星 穂積 (政策研究大学院大学) [概要]
衆議院と参議院の各都道府県への議席配分について,いくつかの観点から考察する.1つ目はジニの平均差を使って,公平性の分析を過去のデータにより行う.2つ目は,配分する議席数に最小値がある場合に,格差はどの程度まで許されるのか,やはり過去のデータを使って考察を行う.
- コンフリクト解決のためのグラフモデル(GMCR)ーエスカレーション回避を考慮したモデルと適用 / ○加藤 有紀子 (東京工業大学) [概要]
国際関係における対立について、紛争の拡大(エスカレーション)回避の視点から、ゲーム理論から派生した枠組みの一つであるコンフリクト解決のためのグラフモデル ( GMCR :The Graph Model for Conflict Resolution)の枠組みを用いて分析し、新たな概念と方法を提案する。
▷ [研究部会OS] 幾何学的形状生成(4) [9月8日:14:50-16:10:A]
- 離散Weierstrass型の表現公式 / ○安本 真士 (大阪市立大学数学研究所) [概要]
この30年間で,微分幾何学的性質を持つ曲面の離散化は様々な研究領域と関わりを持ちながら急速な発展を遂げている.本講演では,離散オメガ曲面に対する変換を利用した,種々の離散曲面に対するWeierstrass型の表現公式の統一的な導出法について紹介する.これは離散極小曲面を始めとする従来の結果を全て包括するものである.
- クリスタライン変分問題に対するエネルギー極小解の一意性について / ○小磯 深幸 (九州大学マス・フォア・インダストリ研究所), 奥田 健斗 (九州大学数理学府) [概要]
結晶やある種の液晶のように異方性を持つ物質は,エネルギー密度が表面の向きに依存する非等方的エネルギーの「体積一定」の条件下での極小解を形作る.非等方的エネルギーの最小解はウルフ図形と呼ばれる凸図形である.ウルフ図形が平坦な面を持つ時,エネルギー密度関数は微分不可な点を持ち古典的な変分法は使えない.本講演では,ウルフ図形がある種の対称性を持てばエネルギー極小解の一意性が成り立つことを報告する.
- 区分的に滑らかな非等方的平均曲率一定超曲面の不安定性について / ○軸丸 芳揮 (九州大学マス・フォア・インダストリ研究所), 小磯 深幸 (九州大学マス・フォア・インダストリ研究所) [概要]
Euclid空間内の区分的に滑らかな超曲面に対する非等方的エネルギー の,囲む体積一定条件下におけるエネルギー最小解はWulff図形とよばれ,十分小さな結晶などの数理モデルとして知られる.
また非等方的エネルギーの囲む体積一定条件下での臨界点は非等方的平均曲率一 定(CAMC)超曲面として特徴づけられる.
本講演では,Wulff図形と異なる区分的に滑らかなCAMC超曲面の存在と,それら のエネルギー不安定性に関する結果を紹介する.
本研究は小磯深幸教授(九州大学IMI)との共同研究に基づく.
- 三浦の三角形(Miura’s Triangle) / ○三浦 憲二郎 (静岡大学), Gobithaasan R.U. (マレーシア大学トレンガヌ校), 關根 惟敏 (静岡大学), 臼杵 深 (静岡大学) [概要]
これまのでBezier 曲線の拡張は,複数セグメント間の接続を強く意図しており,たとえば,始点と終点での接線や曲率連続性を独立に保証するために(必要に応じてさらに形状制御パラメータを追加して)4個の制御点によって曲線を定義することが主流である.この研究動向に反してκ-曲線では端点ではなく曲線上1点での曲率極値の位置を制御するために,3個の制御点より定義される2次Bezier曲線を用いている.本研究では,κ-曲線を拡張する目的で,(sin t, cos t, 1)を基底関数とする一般化三角関数基底を提案するとともに,
その基底関数の係数より生成される Miura’s triangle(三浦の三角形)について詳述する.
▷ [研究部会OS] 応用カオス(3) [9月8日:14:50-16:10:B]
- 2対1での無線電力伝送における送電方式の評価 / ○本山 雅孝 (京都大学大学院’), 梅野 健 (京都大学大学院’) [概要]
無線電力伝送において送電側と受電側で通常1対1で送受電を行っている。今回の講演では送電局を2にしたうえで受電局は1にした場合にどのような物理特性があるか調査したのでこれを報告する。
- レーザーカオスにおけるモードの同時性 / ○桑島 史欣 (福井工業大学), Mona Jarrahi (UCLA), Semih Cakmakyapan (UCLA), ⽩尾 拓也 (福井工業大学), 岩尾 憲幸 (福井工業大学), ⾕ 正彦 (福井⼤遠⾚セ), 栗原 ⼀嘉 (福井⼤教育), 森川 治 (海保⼤), 北原 英明 (福井⼤遠⾚セ), 和田 健司 (大阪府立大), 中嶋 誠 (阪⼤レーザー研) [概要]
レーザーの縦モードが同時に発信しているかを観測できる分光器は現在のところ存在しない。
一方、多モード半導体レーザーによるTHz波発生方法では、モードが同時に発生していることが必須となる。
その元となる、レーザーの縦モード間の光ビートを、他のTHz波源と混合することで、
1GHz程度に下方変換し、モードの同時性を調査したので報告する。
- 特性関数に基づく安定分布則のパラメータ推定手法とその応用 / ○柿中 晋治 (京都大学大学院), 梅野 健 (京都大学大学院) [概要]
安定分布は、金融市場をはじめとする様々な科学分野において、ファットテールや歪度を効果的に記述できることが知られている。安定分布を適用する際の主要かつ困難な問題の一つは、4つのパラメータを正確に推定することである。本研究では、スケール指数と特性関数の相互関係を利用した新しい手法を提案することで、この問題に取り組む。具体的には、特性関数を評価すべき適切な点を柔軟に選択することで、安定分布則の検出を可能にする。
▷ [研究部会OS] 科学技術計算と数値解析(4) [9月8日:14:50-16:10:C]
- ポートハミルトン系に対する高速な構造保存数値解法 / ○大沼 賢矢 (東京大学大学院情報理工学系研究科) [概要]
ポートハミルトン系は制御論の分野などで用いられることがある常微分方程式のクラスである.本研究においては,ポートハミルトン系のうちフィードバックが線形な場合について,Cheng et al.(2019)において提案された勾配流に対する手法を自然に適用し,従来手法よりも高速な構造保存数値解法を構成できることを示す.さらに,フィードバックが線形でない場合に対しての適用方法についても考察する.
- 拘束条件に注⽬したEinstein⽅程式の離散スキームについて / ○星野 秀朋 (早稲田大学), 佐藤 慧 (早稲田大学), 米田 元 (早稲田大学) [概要]
Einstein方程式を数値的に解く際に適した離散スキームを構築したい.そのためには一般的に知られている離散化誤差だけでなく,拘束条件(Constraint)の誤差も考慮する必要がある.これら二つの誤差に基づいてEinstein方程式の数値計算に用いられてきた従来の離散スキームを評価する.さらに,拘束条件の誤差が小さくなるようなスキームの作成法およびそのときの問題点を述べる.
- 凸多角形格子上の積分定理とその証明 / ○降籏 大介 (大阪大学サイバーメディアセンター) [概要]
積分定理の離散化は空間と微積分操作を離散化したものと整合せねばならず,そのために実現される組み合わせには強い制限があった.これまで知られているもっとも制限の少ないものが Voronoi 分割を用いて離散化した空間上に piecewise constant 関数で関数を構成する枠組みであったが,これに対し,任意の凸多角形で空間を分割しての枠組みでも積分定理の離散化が可能である.そしてこの積分定理を示す証明は構成的であり,この枠組みの特徴をたいへん明確に示すものであるのでこれを紹介したい.
▷ [研究部会OS] 連続体力学の数理(2) [9月8日:14:50-16:10:D]
- Reduced-dimension models for nematic elastomer foundations / ○Cesana Pierluigi (IMI, Kyushu University), Leon Baldelli Andres Alessandro (CNRS) [概要]
I will discuss the derivation of the effective (mesoscale) energy density of thin elastic foundations composed of Nematic Liquid Crystal Elastomers (NLCEs) via asymptotic variational analysis (Gamma-convergence). NLCEs are a family of polymeric materials with embedded nematic mesogens. Their mechanical response is governed by the coupling of rubber elasticity with the orientational order of a liquid crystalline phase. NLCE membranes can display fine-scale features both due to wrinkling that one expects in thin elastic membranes and due to oscillations in the nematic director that one expects in liquid crystal elastomers. By computing the exact Gamma-limit of the energy, I show how formation of microstructure interacts with geometrical constraints typical of thin membranes in a variety of limit regimes. Applications are discussed for soft sensors, actuators, wrinkle-free structures. This is a joint work with AAL. Baldelli (CNRS).
- Comparative study of image segmentation techniques by curvature driven flow of graphs / ○Kolar Miroslav (明治大学), 矢崎 成俊 (明治大学) [概要]
In this contribution, we deal with the image segmentation by the curvature driven flow of graphs. We restrict ourselves to the case where the segmented objects can be represented by 1D graphs of functions. Unlike the usual direct approach involving either open or closed moving parametrized curves, our description benefits from certain advantages and simplifications. We discuss three different methods for image segmentation and reformulate them in terms of the curvature driven flow of graphs. Then, all three methods are compared in a qualitative computational study.
- Numerical stability of self-induced velocity on the tent model / ○Lee Yu-Hsun (京大情報), 藤原 宏志 (京大情報), 木村 芳文 (名大多元数理) [概要]
In this research, we investigate the numerical stability of self-induced motion of a tent shape vortex filament by Biot-Savart law which is represented as an integro-differential equation. Our numerical scheme adopts the Runge-Kutta method for time evolution, and the double exponential rule for integration. We establish the numerical stability criteria for this process. Numerical stability of the reconnection phenomenon is also discussed in terms of accumulation of rounding errors.
▷ [研究部会OS] 数理的技法による情報セキュリティ(1) [9月8日:14:50-16:10:E]
- 整数線形計画を用いた差分解読の差分パス探索【OS企画講演 60分】 / ○佐々木 悠 (NTT) [概要]
共通鍵暗号を設計する際、設計者は安全性評価を示す必要がある。特に、最も基礎的な解読法の一つである差分解読に対する安全性は、設計者が最低限評価するべき対象として広く認識されている。近年、様々な演算構造に汎用的に適用できる評価ツールとして整数線形計画を用いた評価手法が広く利用されている。本講演では、差分解読の最適な差分経路探索問題を整数線形計画による最適解探索問題に変換する方法を説明し、ケーススタディとしてAES, SKINNY, Simonなどいくつかのブロック暗号に適用する。
▷ [研究部会OS] 若手の会 [9月8日:14:50-16:10:F]
- 留学と数値解析 【40分】 / ○中務 佑治 (オックスフォード大学) [概要]
講演者は東大ーUC DavisーManchesterー東大ーOxfordーNIIーOxfordと異動しながら現在に至ります.本発表では自身の経験に基づいて、海外の生活、研究、キャリアについて紹介させて頂くつもりです.海外で研究することの利点、欠点について、できるだけ客観的にお話しする予定です.また、講演者の専門である数値解析、数値線形代数、関数近似論について主観的立場から述べます.特に留学を検討している学生や若手研究者の方の参考になれば幸いです.ご質問を歓迎します.質問が無ければ時間が余ると思われるので、その場合は通常の研究の話をする予定です.
- 機械学習の数理研究と統計科学 【40分】 / ○鈴木 大慈 (東京大学/理研AIP) [概要]
現在,機械学習は深層学習の勃興やデータ科学ブームに後押しされ,注目を浴びやすい分野に発展してきた.一方で,そのような流行以前においては機械学習は必ずしも学問分野として高く評価されていたわけではない.本講演では,そのような比較的新興分野である機械学習において研究を進めるようになったきっかけや機械学習分野における研究の進め方に関する特色を述べ,また研究テーマの選択における基本的な考え方などを述べたい.特に,分野の流行度合いがどのように研究の進め方や研究テーマの選択に影響するかについてや,変化のスピードが速い分野における個人的な心構えについても述べてみたい.
▷ [研究部会OS] 幾何学的形状生成(5) [9月8日:16:20-17:40:A]
- 産業利用のための特別なクラスの曲線・曲面 -双方向循環型の形状設計プラットフォームに向けて- 【OS企画講演 80分】 / ○横須賀 洋平 (鹿児島大学), 三谷 純 (筑波大学), 梶原 健司 (九州大学), 小磯 深幸 (九州大学), 大崎 純 (京都大学), 鍛冶 静雄 (九州大学), 前川 卓 (早稲田大学), 三浦 憲二郎 (静岡大学) [概要]
数学、情報科学、設計諸分野の協働によって、可展面などの特別なクラスの曲線・曲面の生成と活用方法を検討し、産業利用を促進するために諸分野における形状設計手法の基盤構築が重要といえる。本パネルディスカッションでは、三谷純先生の折り紙に関する講演と著者の建築に関する講演により、特別なクラスの曲線・曲面の活用法の可能性を概観し、逆方向目的型ソフトウェアや双方循環型の形状設計プラットフォームの議論を行う。
▷ [一般講演] 一般講演(3) [9月8日:16:20-17:40:B]
- 行列多様体上の最適化問題に対する対数写像の近似に基づくアプローチ / ○後藤 潤平 (京都大学), 佐藤 寛之 (京都大学) [概要]
近年,リーマン多様体上の幾何学的距離を目的関数に含む最適化問題の研究が盛んに行われている.リーマン計量から定まる幾何学的距離やその勾配を計算する上でリーマン多様体上の対数写像が必要となるが,扱う多様体によっては計算量が大きいという問題点がある.そこで本研究では,リーマン多様体上の対数写像についてその近似を新たに定義し,特にグラスマン多様体などの行列多様体上の最適化問題に応用することで,計算時間の低減を実現する.
- アジョイントプログラムを利用したデータ同化と観測データ数について ー 拡散方程式での準備的考察 ー / 囲 佳祐 (法政大学 大学院), ○堀端 康善 (法政大学 理工学部) [概要]
1次元拡散方程式を例にとり、最適化を利用したデータ同化と観測データ数の影響について考察する。シミュレーションで生成した擬似観測データを使用して目的関数を定義し,ある時点での温度の完全な情報を推定する問題を最適化問題として定式化する。L-BFGS-B法を用いて最適化を行う。ソースプログラムを微分し,得られたアジョイントプログラムを利用し、目的関数の勾配を計算する。微分には自動微分ツールTAPENADEを使用する。観測点を増やすとより正確な推定値が得られるが、2地点でも厳密値と傾向の似た推定値が得られた。
- GAによる折版構造の剛性と表面積の相関関係の考察 / ○齋藤 魁利 (北九州市立大学), 藤田 慎之輔 (北九州市立大学) [概要]
折紙工学は近年目覚ましい発展を遂げているが,建築構造物の設計においても,折紙工学の知見を利用した事例は多く存在する。特に,曲面材ではなく平面材を利用することが前提となるCLTパネル工法との親和性は高く,多くの実施設計例が存在する。本研究では,CLTパネル工法を想定したアーチ型の折版構造を対象とし,ケーススタディとしてGAにより多目的最適化を行い,特に折版構造の剛性と表面積の関係について考察する.
- 連結ピン組織構造の異なる階層間に伝達長の大きい関係を追加するモデル / ○澤田 清 (流通科学大学) [概要]
高さHの完全K分木の全兄弟を隣接化した完全K分木型連結ピン組織構造に対して,異なる階層の2メンバー間に伝達長の大きい関係を追加するモデルを提案する.すなわち,完全K分木型連結ピン組織構造の各辺の長さ1に対して,追加辺の長さをL(1<L<2)とする.ここでは,辺を追加したときの総頂点間短縮経路長を定式化し,最適な辺追加位置について考察する.
▷ [研究部会OS] 行列・固有値問題の解法とその応用(1) [9月8日:16:20-17:40:C]
- 残差スムージングによるGlobal Krylov部分空間法の収束性改善 / ○相原 研輔 (東京都市大学) [概要]
Global Krylov部分空間法は,連立一次方程式に対するKrylov部分空間法を線形の行列方程式に適用できるよう拡張したものである.本講演では,残差ノルムの振動が起きる短い漸化式を用いた解法群に焦点を当て,残差スムージングを用いて収束性の改善を図る.特に,最近提案された相互作用型の残差スムージングを応用することで,収束振る舞いを滑らかにするだけではなく,近似解精度の向上も同時に達成する手法を示す.
- レトラクションの逆写像を用いた幾何学的共役勾配法の数値線形代数への応用 / ○佐藤 寛之 (京都大学), 竺 筱晶 (上海電力学院) [概要]
行列補完問題や対称行列の近似的同時対角化問題は,リーマン多様体上の最適化問題として定式化することができる.本講演では,こうした最適化問題の解法として,探索方向を計算する際にレトラクションの逆写像を用いるリーマン多様体上の新たな非線形共役勾配法を提案し,その応用について紹介する.さらに,提案手法の大域的収束性などの理論的な議論および,数値実験による有効性の検証を行う.
- エルミート一般化固有値問題に対するBlock SS-Hankel法の固有ベクトル精度改善法 / ○来栖 壮馬 (筑波大学), 今倉 暁 (筑波大学), 櫻井 鉄也 (筑波大学) [概要]
近年,一般化固有値問題に対する周回積分型解法の一つであるBlock SS-Hankel法に対して,エルミート行列向けの改良法が提案された.しかしながら,エルミート行列向けのBlock SS-Hankel法は固有ベクトルの精度は悪化する問題点がある.本研究では,固有ベクトルに対する最小二乗問題に基づき,計算コストを削減しつつ固有ベクトルの精度を向上させる方法を提案する.数値実験から提案法の有用性を確認する.
- 実数シフトのレゾルベント少数で構成されたフィルタを用いた実対称定値 一般固有値問題の下端付近の固有値を持つ固有対の近似解法について / ○村上 弘 (東京都立大学) [概要]
実対称定値一般固有値問題Av=λBvの近似固有対を求めるためのフィルタとして,少数のレゾルベントの線形結合の作用のチェビシェフ多項式を用いる.特性の優れたフィルタを構成できる既提出の方法では,レゾルベントのシフトは複素数であり,複数のシフトを実数だけにすることはできない.そこで今回は,固有値が下端付近にある固有対を求める場合に限定して,フィルタを実数シフトのレゾルベント2つから構成して,それを用いた実験の例を示す.
▷ [研究部会OS] 連続体力学の数理(3) [9月8日:16:20-17:40:D]
- Approximating multi-layer neural network by an optimal control of PDE / ○本多 泰理 (東洋大学 情報連携学部) [概要]
近年ODENET等に見られる様に、ニューラルネットワークを連続体上の時間発展系と見なすアプローチが議論されている。本検討では、多層ニューラルネットワークにネットワークの連続近似を適用し、連続な空間上での偏微分方程式の最適化問題として近似的に定式化し議論を行う。
- ワクチン接種可能数と治療可能数を考慮した感染症流行モデル / ○祇園 大夢 (島根大学), 齋藤 保久 (島根大学), 矢崎 成俊 (明治大学) [概要]
感染症流行モデルの原型であるSIRモデルに,「ワクチン接種」や「治療」というより現実的な条件を加えたモデル方程式の解の挙動について考察する。一般に感染症の予防と治療はその流行を抑制する役割として有効であるが,現実的にはワクチン接種可能数や治療可能数(例えば,病院の寝台数や薬量)には限りがある。本講演では,感染者集団を,治療不要な軽度感染者と治療を要する重度感染者に内分し,ワクチン接種可能数の限度とそれを超えて生じるワクチン非接種者の感染重度性,および重度感染者に施す治療可能数の限度を考慮した感染症流行モデルを提案し,それらの「限度」が感染症流行に及ぼす影響について論じる。
- 3 次元 Helmholtz 方程式に対する境界要素法におけるRWG 基底を用いた Calderon の前処理について / ○田原 寛太 (京都大学情報学研究科), 新納 和樹 (京都大学情報学研究科) [概要]
本研究では, 3 次元 Helmholz 方程式の境界要素法において, RWG 基底を用いた Calderon 前処理を提案した. これまでの研究では, 3次元 Laplace 問題の境界要素法に RWG 基底を用いることで, Calderon の前処理を適用できることが報告されている. 本論文では, この手法を3次元Helmholz方程式に拡張した. また, 提案手法を検証するための数値例を作成した.
▷ [研究部会OS] 数理的技法による情報セキュリティ(2) [9月8日:16:20-17:40:E]
- 多変数多項式暗号方式に対する代数攻撃を用いた安全性解析 / 池松 泰彦 (九州大学), ○中村 周平 (日本大学) [概要]
本研究は耐量子暗号の候補である多変数多項式暗号に関する研究であり, 講演では“Theoretical Computer Science 2020″においてJiahui Chenらにより提案された多変数多項式暗号に対する攻撃手法について説明する. 特に, 線形代数と代数攻撃を組み合わせた攻撃により設定された80-bitパラメータが約25bitsの計算量で解くことができることをみる.
- DeepSecを用いた可換性をもつ関数の形式化 / ○野口 凌雅 (茨城大学), 米山 一樹 (茨城大学) [概要]
DeepSecは,暗号プロトコルに対する識別不可能性を検証する形式検証ツールであり, トレース等価性とセッション等価性を扱うことができ,停止性を保証しているという特徴がある.しかし,文法による制限から指数関数やXOR関数といった可換性をもつ関数の形式化の例は知られていない.本発表では,DeepSecに よる可換性をもつ関数の形式化の提案を行う.
- ProVerifを用いたMD変換の形式化 / ○吉村 東悟 (信州大学), 荒井 研一 (長崎大学大学院工学研究科), 岡崎 裕之 (信州大学), 布田 裕一 (東京工科大学コンピュータサイエンス学部), 三重野 武彦 (エプソンアヴァシス株式会社) [概要]
本稿では,SCIS2020で発表した『ProVerif を用いた MD 変換の形式化』の形式化手法を改善し,パディングの形式化と ProVerif version2.01 でサポートされた 自然数型「nat」を使用した形式化を行った.また,MD 変換による計算結果が暗号学的ハッシュ関数の安全性要件を満たすことを検証する.
▷ [研究部会OS] 数理医学 [9月8日:16:20-17:40:F]
- EphA2とEGFRを介した肝細胞がん悪性化シグナルの数理モデル解析 / ○榎本 将士 (大阪大学 大学院基礎工学研究科), 室井 敦 (神奈川県立がんセンター 臨床研究所), 森 竜樹 (大阪大学 大学院基礎工学研究科), 越川 直彦 (神奈川県立がんセンター 臨床研究所), 鈴木 貴 (大阪大学 数理・データ科学教育研究センター) [概要]
EphA2は細胞膜上に局在する受容体型タンパク質で、肝細胞がん等で過剰発現しておりがん悪性化の促進や転移に関わる。また、膜貫通型タンパク質EGFRとその下流シグナルは、がんの増殖や生存に重要な役割を果たす。近年、EphA2が受ける刺激ephrinの有無によって、EphA2とEGFRのシグナル経路が複雑に相互作用し、「がん促進」と「がん抑制」の相反する寄与が明らかとなった。しかし、詳細な分子機序は不明である。今回は、これらの反応系に関する数理モデルを構築し実験結果との比較検討から解析した結果を報告する。
- 一時的不活性化による成長ネットワークの頑健性向上 / ○小串 典子 (大阪大学) [概要]
生態系や社会、腸内細菌叢といった現実の大規模複雑系の特徴は、外からの新規要素の流入と相互作用による既存要素の消滅という擾乱に常に晒されつつ成長する系であるという点であり、この観点から、系を要素間直接相互作用により構成される成長ネットワークと見做すことができる。本公演では直接相互作用に基づき成長するネットワークモデルを用い、要素の一時的不活性化が系の頑健性に対して与える影響について報告する。
- 複数の変数で表現された変量について、2時点における変量の値と各変数の値を観測したとき、変量の観測値の差への各変数の寄与を公平に推定する一つの統一的な方法について / ○村山 令二 (健康保険組合連合会) [概要]
医療費分析等の実務では、例えば、6変数で表現される変量F(x,y,p,q,u,v)=xpu+yqv について、6変数が時間の関数で、2時点t0,t1(t0<t1)における変量の値と6変数の値を観測したとき、2時点における変量の観測値の差に対する6変数それぞれの寄与分を、変量の観測値の差を線形近似したり変数に優先順位をつけたりすることなく、公平に推定する。これは、1つの統一的な推定方法であり、各変数を未知関数とするある連立常微分方程式の逆問題の解を用いる。
- 非アルコール性脂肪性肝疾患に対する数理モデルを用いた新たな病理診断法開発 / ○鎌田 佳宏 (大阪大学大学院医学系研究科生体病態情報科学), 鈴木 貴 (大阪大学数理・データ科学教育研究センター(MMDS)), 三善 英知 (大阪大学大学院医学系研究科生体病態情報科学) [概要]
非アルコール性脂肪性肝疾患(NAFLD)は肥満人口の増加に伴い、世界中で増加している慢性肝疾患である。NAFLDの1~2割の症例は非アルコール性脂肪肝炎(NASH)と呼ばれ、肝硬変、肝癌発症へと進行する。NAFLDからNASHを鑑別する方法は肝生検による組織診断がゴールドスタンダードである。その際、ballooning hepatocyte(BH)という膨化した肝細胞の存在診断が重要であるが病理医によってその診断にバラつきがあることが問題である。今回数理モデルを用いてBH病理診断法の開発を行ったので報告する。
▷ [研究部会OS] 行列・固有値問題の解法とその応用(2) [9月9日:09:10-10:30:A]
- 特異系に対するGMRES法とRRGMRES法の収束解析 / ○杉原 光太 (国立情報学研究所), 速水 謙 (国立情報学研究所 総合研究大学院大学) [概要]
辺要素有限要素法を用いた電磁場解析等で生じる特異系において,右辺が係数行列の値域に属さない場合,丸め誤差に強いGMRES法とRange Restricted GMRES (RRGMRES)法の収束性を,理論および特異対称系に対する数値実験により比較する.
まず収束性をアルゴリズムを像空間とその直交補空間の成分に分離することにより証明する.さらにGMRES法が数値的に収束が困難な原因はHessenberg行列の最小特異値が微小になるためである事を示し,その理由を示す.
- ノイズを含むデータに対する動的モード分解の推定精度の理論解析 / ○相島 健助 (法政大学情報科学部) [概要]
動的モード分解とは,時系列データを解析する有用な技術であり,数値線形代数の観点からは,行列の特異値分解およびレイリー・リッツの技法を用いて主要な固有対を求める計算手法と解釈できる.本発表では,ある種の確率的なノイズを含む場合の行列データに対する動的モード分解に対して理論解析を行い,求めるべき不変部分空間への確率的な意味での収束速度を示す.
- Shift-invert Arnoldi法による作用素ベクトル積近似の収束性解析 / ○橋本 悠香 (NTT / 慶應大学), 野寺 隆 (慶應大学) [概要]
近年,時系列データ解析の手法のひとつに,データが非線形力学系から生じたものと考え,力学系の時間発展を表すPerron-Frobenius作用素を推定する方法が注目を集めている.Perron-Frobenius作用素は,Hilbert空間上の線形作用素として定義されるため,これを推定するためのKrylov部分空間法が利用できる.一般的には,線形作用素をあるベクトルへ作用させたものをKrylov部分空間上で近似する問題となる.本発表では,Krylov部分空間法としてShift-invert Arnoldi法を適用した場合の収束性解析を行う.
- 最小作用の原理における作用積分の不定値性について / ○鷲尾 巧 (UT-Heart研究所) [概要]
最小作用の原理では, 力学系の運動は作用積分を最小にする軌道に沿うと主張する. しかし現実にはポテンシャルによっては一定の時間の後に古典軌道の最小性は失われ単なる極値点に変化する. 本講演では行列の固有値解析によりどのようにして不定値性が現れるのか考察する. さらに作用積分の不定値性が量子力学におけるファインマンの経路積分にどのような影響を与えうるか調和振動子を例に考える.
▷ [研究部会OS] 離散システム(1) [9月9日:09:10-10:30:B]
- Paley行列のrestricted isometry propertyとPaleyトーナメントに関するグラフ理論的問題 / ○佐竹 翔平 (熊本大学 大学院先端科学研究部 (工学系)) [概要]
Paley行列は有限体の平方剰余から構成される複素行列です. Bandeira, MixonおよびMoreiraは, ある数論的予想の下で, 位数が4n+1型の素数である有限体上のPaley行列が, 従来の制約を打破するRIP (restricted isometry property)をもつことを示しました.
本講演では4n+3型の素数の場合に, 同様の予想の下で, Paley行列が制約を打破するRIPをもつと同時に, Paleyトーナメントに関するいくつかの結果もあわせて得られることを示します.
- On p-frame potential of determinantal point processes on the sphere / ○平尾 将剛 (愛知県立大学) [概要]
近年,確率点過程の中でも行列式点過程の応用研究に関心が高まっている.本講演では行列式点過程の中でもその典型例である球面アンサンブル,調和アンサンブル,およびジッタードサンプリグに着目し,そのランダム点配置が持つp-フレーム・ポテンシャルの期待値の評価を行う.さらにその応用の一つとして,球面上の一様分布から生成されるランダム点配置と比べ,これら行列式点過程の生成するランダム点配置がタイト・フレームを近似する良い点配置であることを示す.
- ブロック暗号のS-box変換のサイクル分解が与える安全性への影響 / ○山本 ひなの (お茶の水女子大学大学院), 島村 香帆 (お茶の水女子大学大学院), 萩田 真理子 (お茶の水女子大学) [概要]
これまでに偏りのあるデータの集合を暗号化した際の暗号文の偏りを検出することで暗号の乱数性を評価してきた.
本研究では,AES暗号の変換の1つであるSubByte変換を置換としてサイクル分解することで得られたサイクルに注目した偏りを持たせることで,0の多いテータの集合を用いたときと比べて偏りが検出しやすくなることに着目し,ブロック暗号のS-box変換のサイクル分解が暗号の安全性に与える影響について紹介する.
- マルコフ連鎖準モンテカルロ法の応用 / ○原瀬 晋 (立命館大学理工学部) [概要]
MCMC法を用いた期待値計算に対して、乱数を準乱数に置き換えて、収束性の向上を図りたい。しかし、通常の準乱数は、そのまま適用することが出来ない。近年、CUD列を用いると、期待値の一致性が示されたが、その定義は構成的でない。発表者は、Tausworthe発生法に着目し、一様性の指標であるt-値の最適化を行い、CUD近似点集合を得た。本講演では、この点集合の概要を述べ、MCMCの数値実験、特に、ベイズ統計学の数値計算への応用を紹介する。
▷ [正会員OS] 応用力学系(1) [9月9日:09:10-10:30:C]
- トーラス上の面積保存写像の母関数の多価性と周期点の個数評価 / ○柴山 允瑠 (京都大学) [概要]
面積保存写像の研究において,円環領域上のツイスト写像の場合は,変分法により不変な閉曲線の存在が示されている(Aubry-Mather理論).一方,双曲的な面積保存写像の軌道の振る舞いは記号力学系を通して理解することが可能である.
本講演では,双曲的な場合も含む面積保存写像に対する変分解析を行う.この場合,母関数が無限多価関数となり,写像を合成するごとに対応する母関数の分枝を取り方を変えることで,多くの周期点の存在を示すことができる.
- 平面円制限3体問題における多様な周期解の存在証明 / ○梶原 唯加 (京都大学大学院情報学研究科), 柴山 允瑠 (京都大学大学院情報学研究科) [概要]
質量0の質点が平面上を円運動する2質点から万有引力を受けて運動するときの振る舞いを調べる問題を平面円制限3体問題という.本講演では,平面円制限3体問題の変分問題としての定式化において6種類の境界条件を考え,それぞれの場合のminimizerについて考察する.minimizerの存在条件,それが定常解とは異なるための条件を確認し,さらに局所評価と呼ばれる手法を用いることで解の特異性を除去することで対称性を持った6種類の周期軌道の存在を示す.
- 等質量3体8の字解から分岐する非平面解 / ○福田 宏 (北里大学), 藤原 俊朗 (北里大学), 尾崎 浩司 (東海大学) [概要]
等質量3体8の字解において,相互作用ポテンシャルの次数aを変化させると,8の字解がいくつかのaで同じ周期の周期解に分岐する。a=0.9966から分岐する周期解は,a=1でSimóの発見したH解に至るが,その周期解をaが小さい方に追跡してゆくと,a=0.8460で非平面周期解に分岐する。群論的分岐理論によれば,8の字解から分岐する非平面周期解の対称性は4種類可能だが,現在のところ,次数aをパラメタとした追跡では,非平面周期解への分岐はこのa=0.8460しか見つけていない。
- 近可積分系における第一積分の存在のための必要条件 / ○本永 翔也 (京都大学大学院情報学研究科), 矢ヶ崎 一幸 (京都大学大学院情報学研究科) [概要]
力学系の可積分性の判定は,可積分系に小さな摂動が加えられた近可積分系に対しても未だ困難な問題となっている.本講演では,系の次元分の個数の第一積分または可換なベクトル場の存在を要求するBogoyavlenskijの可積分性の定義を採用し,一般的にハミルトン系でない近可積分系に対して,もとの可積分系と同じ個数の第一積分が存在するための必要条件を与える.また,周期外力を受ける1自由度ハミルトン系に対して,本結果と分数調波軌道のメルニコフの方法との関連についても触れる.
▷ [研究部会OS] 応用可積分系(1) [9月9日:09:10-10:30:D]
- アフィン型ミューテーションの周期性と線形化 / ○野邊 厚 (千葉大学), 松木平 淳太 (龍谷大学) [概要]
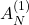 型ミューテーションから自然に導かれる双有理写像力学系を考察する。このとき交換行列は自明な周期性をもつが、クラスター変数や係数から構成される単項式の中にも同様の周期性をもつものが存在し、このような周期性を利用することで双有理写像力学系が線形化できることを示す。さらに、線形化を通して双有理写像力学系の一般解を求める。
型ミューテーションから自然に導かれる双有理写像力学系を考察する。このとき交換行列は自明な周期性をもつが、クラスター変数や係数から構成される単項式の中にも同様の周期性をもつものが存在し、このような周期性を利用することで双有理写像力学系が線形化できることを示す。さらに、線形化を通して双有理写像力学系の一般解を求める。
- 超離散BKP方程式のソリトン解について / ○新澤 信彦 (西日本工業大学), 長井 秀友 (東海大学) [概要]
前回までの講演で,係数を一般化した離散BKP方程式のソリトン解を求めた。今回はこのソリトン解が常に正になる為の条件を求め,その結果を活用して超離散BKP方程式のソリトン解を求める。超離散BKP方程式には3種類のソリトン解がある事を示し,異なった種類のソリトンが混在出来る事,又,これらのソリトンの性質を紹介する。
- 一次元力学系における超離散方程式について / ○大森 祥輔 (早大理工), 山崎 義弘 (早大理工) [概要]
一次元の非線形ダイナミクスにおけるサドルノード、トランスクリティカル、ピッチフォーク分岐を示す3つの標準型の非線形方程式に対し、それらの超離散方程式を導出し、得られた超離散方程式と元の標準型との間で、固定点の安定性、分岐について比較する。また、各超離散方程式に対応する簡単なmax-plus離散方程式を提案し、グラフ解析を行うことで、超離散方程式の動力学的性質を考察する。
- 整数行列の単因子を計算する超離散可積分系 / ○小林 克樹 (京都大学 情報学研究科), 辻本 諭 (京都大学 情報学研究科) [概要]
単因子とは単項イデアル整域上の行列(特に整数行列)に対して定まる不変量の一つであり,数論やホモロジー群の計算などに多くの応用がある.本発表では,1990年に導入された高橋・薩摩の箱玉系と等価な超離散戸田方程式を用いて二重対角行列の単因子を計算できることを示す.さらに,このアルゴリズムが離散基本戸田軌道と呼ばれる可積分系の族に対して一般化されることを紹介する.
▷ [正会員OS] 位相的データ解析(1) [9月9日:09:10-10:30:E]
- Stable volumes for persistent homology / ○大林 一平 (理化学研究所) [概要]
本講演ではパーシステントホモロジーを使ったデータ解析に有用なstable volumeという概念を定式化し,その数学的性質や計算法,実際の計算例について講演する.パーシステント図の各点に対応するホモロジー的構造を再現する(逆解析)はパーシステントホモロジーに有効だが,入力に対して「大きめ」の構造を出力してしまう場合が多い.これは逆解析の安定性と深い関係がある.これに対する既存研究しては確率的な手法を用いる方法がすでに提案されているが,ここではそれとはまた別のstable volumeという概念を提案する.
- 多目的最適化の解集合のトポロジーの検定法 / ○濱田 直希 (KLab株式会社) [概要]
多目的最適化において,問題が単体的であればパレート解集合とパレートフロントの近似超曲面を少数の解から構築できることが知られている.しかし,どのような問題が単体的であるかは,限られた問題クラスでしかわかっていなかった.本研究では,問題クラスが未知であっても,パレート解集合のサンプルが与えられれば,パーシステントホモロジーを用いて問題が単体的であることを統計的に検定する方法を提案する.
- PersLay: A Neural Network Layer for Persistence Diagrams and New Graph Topological Signatures / Carrière Mathieu (Columbia University), Chazal Frédéric (Inria Saclay), ○池 祐一 (富士通研究所), Lacombe Théo (Inria Saclay), Royer Martin (Inria Saclay), 梅田 裕平 (富士通研究所) [概要]
パーシステント図のベクトル化は位相的データ解析を機械学習と組み合わせる際に重要であり様々な手法が提案されているが,それらは予め設定したベクトル化を行うものが主流でデータのラベルを有効に用いることができなかった.本講演ではパーシステント図のベクトル化をニューラルネットワークの一部として捉えてベクトル化を学習させる研究,およびグラフ分類への応用について紹介する.
- 深層学習とパーシステントホモロジーによるハイブリッド画像解析 / ○鍛冶 静雄 (九州大学マス・フォア・インダストリ研究所) [概要]
畳み込みニューラルネットワーク(CNN)は画像解析において非常に強力である一方で、近視眼的でありテクスチャーなど局所的な情報に捉われるすぎる傾向があることが知られている。これは、人間がものを見る時により大域的な手がかりを重視するのと対照的である。本講演では、パーシステントホモロジーによって画像の大域構造を、CNNが学習しやすい形にエンコードする手法を紹介する。
2通りのものの見方を融合することで、実際に画像認識精度が向上することを例示する。
▷ [研究部会OS] 行列・固有値問題の解法とその応用(3) [9月9日:10:40-12:00:A]
- Oakbridge-CXにおけるPipelined CG法へのAMG前処理の適用 / ○依田 凌 (東京大学), 中島 研吾 (東京大学), 藤井 昭宏 (工学院大学) [概要]
高並列環境における集団通信関数は,十数段の通信回数が必要となり通信時間が増大するため,通信回避アルゴリズムが重要である. Ghysels等は非同期集団通信を用いて内積計算のための集団通信を隠蔽するPipelined CG法を提案した. 本研究ではSmoothed Aggregationに基づくAMG前処理をPipelined CG法に適用し,Oakbridge-CXにおける評価結果を紹介する.
- 縦長行列の列ピボット付きQR分解に対するコレスキーQR型アルゴリズムの検討 / ○深谷 猛 (北海道大学), 中務 佑治 (オックスフォード大学), 山本 有作 (電気通信大学) [概要]
列ピボット付きQR分解は,Rank Revealing QR分解の計算等に用いられ,行列の低ランク近似等の応用を持つ。一方,近年,縦長行列のQR分解(列ピボットなし)に対して,コレスキーQR型のアルゴリズムの有効性が,高性能計算の分野で確認されている。そこで,本発表では,縦長行列の列ピボット付きQR分解に対するコレスキーQR型アルゴリズムを検討し,数値実験によりアルゴリズムの性能を検証する。
- カーネルリッジ回帰へのBLR行列近似の適用法検討 / ○伊田 明弘 (東京大学), 今倉 暁 (筑波大学) [概要]
カーネルリッジ回帰は、教師あり機械学習法の一種である。カーネルリッジ回帰では、グラム行列を係数行列に持つ連立一次方程式を解く必要がある。通常、グラム行列は密行列であり、連立一次方程式の求解には、O(N^2) の計算機メモリとO(N^3)の演算量が必要になる。本研究では、グラム行列をBLR行列(低ランク構造行列の一種)で近似し連立一次方程式を求解することにより、O(N ^1.5) の計算機メモリとO(N^2)の演算量で、カーネルリッジ回帰を行う手法を検討する。
- 特異な大規模疎行列の4倍精度演算を用いたLU分解 / ○鈴木 厚 (大阪大学 サイバーメディアセンター) [概要]
複合材料による弾性体方程式や半導体問題のドリフト拡散方程式の離散化で得られる大規模疎行列の条件数は非常に大きくなることが知られている. 並列計算向けの手法であるFETI領域分割法では部分領域の人工境界にNeumannデータを与えるため, 部分剛性行列は特異になる. 条件数が大きい場合はLU分解の過程で浮動小数点演算による擾乱のため, 行列のランクの数値的な決定が難しくなる. 行列に対するスケーリング前処理とピボット遅延部分の高精度演算のための4倍精度演算の活用により DOI:10.1002/nme.4729 で提案したアルゴリズムの適用範囲を拡大できることを示す.
▷ [研究部会OS] 離散システム(2) [9月9日:10:40-12:00:B]
- 有向距離空間上の最小ゼロ拡張問題 / 平井 広志 (東京大学), ○水谷 隆平 (東京大学) [概要]
最小ゼロ拡張問題とは,距離の定まった有限集合上に新たにいくつかの要素を配置するときに,すべての2要素の組についてのコストと距離の積の和の最小値を求める問題であり,最小カット問題,多分割カット問題などを含む問題である.この問題は多項式時間可解である場合とNP困難である場合があるが,それは有限集合上で定まっている距離に依存する.距離が対称である場合については,Hirai(2016), Karzanov(1998)により多項式時間可解かNP困難かのクラス分けが完了している.本発表では,距離が対称とは限らない場合のクラス分けを紹介する.
- 整数計画における遷移問題の計算量 / ○木村 慧 (埼玉大学), 鈴木 顕 (東北大学) [概要]
本講演では,整数計画の遷移問題,すなわち,整数計画問題とその二つの実行可能解が与えられた際に,一方の解からもう一方へ,実行可能性を保ちながら段階的に変換することで遷移できるか否かを判定する問題を扱う.ここで,一度の変換においては,一つの変数への値の割当を変えることのみが許される.この問題は一般にはPSPACE困難となるため,本講演では,整数計画の部分クラスにおける計算量を解析する.
- 群対称テンセグリティの普遍剛性 / ○大場 亮俊 (東京大学), 谷川 眞一 (東京大学) [概要]
テンセグリティとは、棒材・ケーブル・ストラットのピン接合により構成される構造物である。テンセグリティが普遍剛性を持つとは任意の次元において剛であることをいう。超安定性という条件が普遍剛性の十分条件であることが知られていた。我々は一般性の仮定のもとでこれらの等価性を示した。
- グラフ上の極大
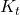 マトロイド予想 / ○谷川 眞一 (東京大学) [概要]
マトロイド予想 / ○谷川 眞一 (東京大学) [概要]完全グラフ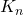 の辺集合上のマトロイド
の辺集合上のマトロイド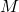 を考える.
を考える.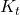 と同型な任意の部分グラフの辺集合が
と同型な任意の部分グラフの辺集合が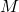 のサーキットであるとき,
のサーキットであるとき,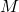 を
を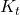 マトロイドとよぶ.
マトロイドとよぶ.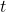 と
と を固定したとき,
を固定したとき,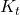 マトロイドの集合上での弱順序に対し,極大なものを極大
マトロイドの集合上での弱順序に対し,極大なものを極大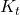 マトロイドとよぶ.本発表では,極大
マトロイドとよぶ.本発表では,極大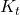 マトロイドの特徴付けに関するGraverとWhiteleyの予想を紹介し,Clinch-Jackson-Tanigawaによる
マトロイドの特徴付けに関するGraverとWhiteleyの予想を紹介し,Clinch-Jackson-Tanigawaによる の場合の解法を紹介する.
の場合の解法を紹介する.
▷ [正会員OS] 応用力学系(2) [9月9日:10:40-12:00:C]
- 自然な距離を持たない相空間における力学系の大域アトラクタについて / ○西口 純矢 (東北大学 材料科学高等研究所) [概要]
無限次元力学系において大域アトラクタは,力学系の散逸性の下で最大のコンパクト不変集合を得るための処方箋である.無限次元力学系として距離空間上の連続時間または離散時間の半流れを考えることは自然であるが,可算個のセミノルムによって位相が定まるフレシェ空間のように,距離化可能ではあるが自然な距離を持たないような空間上の半流れを考えることができる.本講演では,一般の位相アーベル群を時間集合に持つ半流れに対して漸近コンパクト性の概念を導入する.また,擬距離の族により位相が生成されるゲージ空間において,その距離化可能性と正の時間集合の点列性の下で,距離空間上の半流れに対する大域アトラクタの存在定理の拡張を試みる.
- Runge-Kutta法によるMorse分解の近似計算 / ○宮路 智行 (京都大学数学教室) [概要]
Conley-Morseグラフの手法はset-orientedな数値計算によって力学系の相空間構造を回帰的な不変集合とそれらの間の勾配的な構造として記述する.精度保証付き数値計算を用いることで力学系の大域的構造の数学的に厳密な外近似を得ることができる.しかし,常微分方程式で定義される力学系に対して適用する場合,初期値問題を精度保証付き数値計算で解く計算コストとラッピングエフェクトによる検証区間の過大評価という実用上の困難がある.我々は近似計算に基づいてMorse分解を計算する方法を提案する.数学的な厳密性は犠牲になるものの,相空間構造を理解する上での実用性を向上することができるだろう.
- 複数のスパースグラフに依存する結合振動子ネットワークの連続極限 / 伊原 亮輔 (株式会社クボタ), ○矢ヶ崎 一幸 (京都大学) [概要]
連続極限は結合振動子ネットワークを解析するための有用な手法として知られている.本講演では,複数のスパースグラフに依存する結合振動子ネットワークを取りあげ,連続極限の方法がまた有効であることを示す.さらに,蔵本タイプの結合振動子系に対して本結果の有用性を確認する.
- 非線形写像の2次元連成系での大域収束性を混合ガス分離へ応用する試み / ○渡邊 辰矢 (茨城大), 斎木 匠 (芝浦工大), 小野 直樹 (芝浦工大), 松本 壮平 (産総研) [概要]
入出力関係が一対の2次写像で表される素子を2次元格子に並べた系は、連続極限で粘性 Burgers 方程式で近似され、無流束境界条件のとき平衡解に大域収束する。この観察をもとに、温度差を与えた平板間を流すだけで混合流体の成分を分離する2次元ネットワーク(カスケード)を作成した。素子形状と流速を数値計算で最適化し、約2万素子からなるデバイスを作り、水素と二酸化炭素がほぼ1:1の混合ガスを流したところ、160度の温度差の下で出口では9%程の水素濃度分離を観察した。まだ素子や加熱・冷却方法の改善が必要だが、完全な分離に近づける見通しを得た。
▷ [研究部会OS] 応用可積分系(2) [9月9日:10:40-12:00:D]
- 有理型 Heun 作用素の古典類似について / ○辻本 諭 (京都大学情報学研究科), Vinet Luc (Montreal大学数学研究センター), Zhedanov Alexei (中国人民大学情報学部) [概要]
[(n-1)/n] 型有理関数を [n/(n+1)] 型有理関数にうつす最も一般的な2階差分作用素として有理型 Heun 作用素を導入した後,その古典類似と退化から得られる双直交有理関数系について議論する.また,類似の差分作用素との関係についても明らかにする.
- 箱容量Lの箱玉系の線形化手法について / ○前野 温志 (京都大学大学院情報学研究科), 辻本 諭 (京都大学大学院情報学研究科) [概要]
箱玉系は1990年にソリトン性を持つセルオートマトンとして導入された系であり,特に箱容量が1である高橋・薩摩の箱玉系はアーク則と呼ばれる組合せ論的手法を用いることで線形化できることが知られている.本発表では箱容量をLに拡張した場合の箱玉系の線形化について述べる.また,箱玉系の従属変数の取りうる値を一般の整数値に拡張する問題についても考察する予定である.
- 歪直交Laurent多項式とシンプレクティック行列 / ○三木 啓司 (気象大学校) [概要]
直交多項式は3重対角行列の固有値問題の解を与えることが知られており,直交多項式の拡張についてもある種の行列の固有値問題と対応することが知られている。
本発表では,シンプレクティック行列の固有値問題の解として,あるクラスの歪直交多項式の変形が現れることについて述べる。
- 離散2次元戸田方程式に基づく逆固有値問題の解法を用いた帯TN行列の作成方法 / ○岡鼻 小春 (京都産業大学), 赤岩 香苗 (京都産業大学) [概要]
逆固有値問題とは,指定した固有値を持つ行列を作成する問題である.先行研究では,帯行列の逆固有値問題に対して離散2次元戸田方程式に基づく解法が提案されている.その解法では固有値以外にパラメタをいくつか指定できるが,どのようにパラメタを設定すれば,全ての小行列式が非負である行列(TN行列)を作成できるかはわかっていない.本講演では,同解法によりTN行列を作成するためのパラメタの設定方法を提案する.
▷ [正会員OS] 位相的データ解析(2) [9月9日:10:40-12:00:E]
- 心血流エコーVFMデータの流線トポロジカルデータ解析 / ○坂上 貴之 (京都大学), 板谷 慶一 (京都府立医科大学) [概要]
心血流エコーやMRIから得られる心臓左心室内部の流れの画像データに対して適用できる流線トポロジカルデータ解析の数学理論を完成した.本理論により与えられた心臓超音波VFM(Vector Flow Mapping)画像でみ左室心尖部長軸断面の血流画像から特徴的な流れの位相構造を抽出して数学的に分類,さらにそのパターンに固有の文字列表現(COT表現)を割り当てることに成功した.これにより,COT表現によって心臓血流内部の渦流領域として「位相渦構造」が客観的に定義でき,この位相渦構造を用いることで健常例や心不全例における渦流の違いを明確に区別することが可能になった.
- Generalizations of Morse graphs of flows / ○横山 知郎 (京都教育大学) [概要]
力学系や流れのデータを解析するために,MorseグラフとHamilton曲面流のReebグラフを精密化して得られる抽象軌道空間と呼ばれる位相不変量を紹介する.また以下の流れのMorseグラフは一点集合だが,抽象軌道空間は一般に非自明なことを観察する:(1)Hamilton曲面流;(2)周期的同相写像の懸垂流;(3)pseudo-Anosov同相写像の懸垂流;(4)Devaneyの意味でのカオス流
- グリッドデータの劣位合併木の隣接近傍への依存性 / ○宇田 智紀 (東北大学材料科学高等研究所) [概要]
グリッド上の実数値関数の劣位集合が為す増大列の0次パーシステントホモロジーは合併木と呼ばれ,トポロジカルフローデータ解析などへの応用がある.合併木はinterleaving距離に関する安定性が成り立つことが知られる.一方,データのグリッド構造への依存性は明らかではない.そこで,異なるグリッド構造から得られる合併木間のinterleaving距離が十分小さな定数で上から評価できることを示す.
- 岩石内の流れを推定するパーシステントホモロジー / ○鈴木 杏奈 (東北大学), 宮澤 美幸 (東北大学), 大林 一平 (理化学研究所), 平岡 裕章 (京都大学), 伊藤 高敏 (東北大学) [概要]
岩石内の流れは、き裂構造に支配される。本研究では、き裂構造と流動特性との関係を理解するために、き裂ネットワークパターンの解析にパーシステントホモロジーを適用した。3次元のき裂ネットワークパターンを複数生成し、数値シミュレーションによって浸透率を計算した。また、パーシステントホモロジーによってき裂ネットワーク内のき裂開口分布、流路を評価することで、き裂ネットワークの浸透率を推定した。その結果、浸透率の推定値はシミュレーションで得られた浸透率とほぼ同じであった。パーシステントホモロジー解析によって、構造データから物理的な流動が予測できることを示すことができた。
▷ [正会員OS] 感染症の数理モデル [9月9日:13:20-14:40:A]
- COVID-19の流行初期のデータによる予測とその評価 / ○國谷 紀良 (神戸大学大学院システム情報学研究科) [概要]
本講演では,日本の新型コロナウイルス感染症(COVID-19)の流行初期の新規感染者報告数のデータに対して,SEIRモデルを適用することで得られた流行予測の結果を紹介する.その際,本格的な活動自粛が開始する前の2月末までのデータを利用し,流行の強さを表す基本再生産数Roの推定を行う.また,4月7日に発令され,5月25日に解除された日本の緊急事態宣言の防疫効果の検証を併せて行う.
- 新型コロナウイルス感染症に対する感受性の年齢依存性の考察 / ○大森 亮介 (北海道大学), 松山 亮太 (広島大学), 中田 行彦 (青山学院大学) [概要]
2019年12月に中国で新型コロナウイルス感染症(COVID-19)が確認されて以来、その流行は急速に世界に広まりパンデミックとなっている。興味深いことに、イタリア、スペイン、日本の間で、死亡者数が大きく異なるが、死亡者の年齢分布は非常に近い。この状況を理解するために、COVID-19感染症の伝搬動態と自然史を記述した数理モデルを構築したところ、COVID-19感染症に対する感受性の年齢依存性では3カ国の死亡者の年齢分布を説明できない事が示唆された。
- 時間遅れをもつ抗原検査によるCOVID-19流行モデルにおける振動解について / ○竹内 康博 (青山学院大学) [概要]
感染症流行数理モデルとして、いわゆるKermack-McKendricモデルがよく知られている。このモデルでは、基本再生産数が1より大きい場合、感染者数は単調に増加しピーク値に達した後、単調に減少する。すなわち、感染者数は時間に関して振動しない。一方、COVID-19においては、感染者数に振動が見られる。本講演では、PCR検査が実施されるためには感染後一定の時間が必要であることに注目して、Kermack-McKendricモデルを改訂し、この時間遅れによって、振動解の出現可能性に関して議論する。
- 移動境界を持つSIRモデルの進行波解について / 江夏 洋一 (東京理科大学理学部応用数学科), 石渡 恵美子 (東京理科大学理学部応用数学科), ○牛島 健夫 (東京理科大学理工学部数学科) [概要]
拡散項をもつ単純なSIRモデルに,感染地域と未感染地域の境界を記述する移動境界を導入した数理モデルを考える.このモデル方程式の進行波解の存在・非存在と感染症の未感染地域への侵入成功・失敗がどのように方程式のパラメータに依存するのかを論じる.
▷ [研究部会OS] 離散システム(3) [9月9日:13:20-14:40:B]
- M凸関数最小化問題に対する最急降下法の反復回数の解析 / ○南川 智都 (東京工業大学), 塩浦 昭義 (東京工業大学) [概要]
M凸関数は,最小木問題,最小凸費用流問題,離散資源配分問題などの解きやすい組合せ最適化問題の統一的枠組を与える.
M凸関数最小化問題は基本的な最急降下法を用いて有限回の反復で最小解を求められることが知られている.
近年,この問題に対する最急降下法の厳密な反復回数が得られた.
しかし,このバウンドはある種の制約つきM凸関数最小化問題に関する定理の系として得られたものである.
本研究では最小解カット定理の精緻化により,このバウンドの直接的な別証明を与える.
さらに,M凸関数最小化問題の拡張であるジャンプM凸関数最小化問題に対して,基本的な最急降下法の厳密な反復回数を示す.
- コストスケーリングによる行列式の次数の計算について / ○平井 広志 (東京大学大学院情報理工学系研究科), 池田 基樹 (東京大学大学院情報理工学系研究科) [概要]
A = A_1 x_1 t^c_1 + A_2 x_2 t^c_2 + … + Am x_m t^c_mとかける行列のDieudonne行列式の次数計算を考える.ここで,A_iたちは,体上のn x n行列で,x_iたちは互いに非可換な変数で,変数 tとは可換とする.c_iは整数とする.この問題は,重み付き線形マトロイド交差問題などの一般化とみなすことができる. 本発表では,問題の背景にある離散凸性とc_iをコストをみなしたコストスケーリングを利用することで,Dieudonne行列式の次数が,nとmとlog max_i |c_i|の多項式時間でもとまることを示す.
- 線形マトロイド交叉・パリティ問題における数え上げ / 大城 泰平 (東大), ○的矢 知樹 (東大) [概要]
Webb (2004)は,正則マトロイドの対であって,行列木定理を通して共通基の数え上げを行えるクラスとして,パフィアンペアの概念を導入した.また、平面グラフに代表されるパフィアンなグラフ上の完全マッチングの個数はタット行列のパフィアンと等しい。これらの問題の一般化としてパフィアンなマトロイドパリティ上のパリティ基の数え上げを導入する。また、最小重みパリティ基の個数は多項式時間での計算が可能であることを示す。
- 作用素スケーリングに対する情報幾何 / 松田 孟留 (理研), ○相馬 輔 (東京大学) [概要]
作用素スケーリングは(Gurvits 2004)によって行列スケーリングの非可換版として導入された問題で,Edmonds問題やBrascamp-Lieb不等式への応用が近年見つかりつつある.元々,行列スケーリングは情報幾何との密接な繋がりがあり,例えば行列スケーリングの代表的なアルゴリズムであるSinkhorn反復は,Fisher計量に対する交互e射影に一致する.ところが,作用素スケーリングにおいて同様の情報幾何的な解釈ができるかは分かっていなかった.本研究では,作用素スケーリングの代表的アルゴリズムである作用素Sinkhorn反復が,量子情報幾何で知られているSLD計量に対する交互e射影に一致することを示す.
▷ [一般講演] 一般講演(4) [9月9日:13:20-14:40:C]
- 面勾配の変化量を用いた四角形要素で構成される離散曲面の形状制御汎関数の提案 / ○藤田 慎之輔 (北九州市立大学), 齋藤 魁利 (北九州市立大学) [概要]
建築設計の世界において,複雑な曲面はパラメトリック曲面として連続的に扱うのが一般的であるが,格子グリッドで構成されるラチスシェルなどは,実際には連続ではなく離散曲面である。本研究では,四角形グリッドで構成される離散曲面に対して面勾配の変化量をものさしとした汎関数を定義し,同関数を制御することで滑らかでかつ設計上も好ましい曲面を生成可能であることを示す。
- 傾斜変化を伴うカーブの曲率誤認の危険性 / ○杉原 厚吉 (明治大学) [概要]
傾斜が変化しながらカーブする道路を走るドライバーにとって、傾斜の変化に気付かないとカーブの曲率を誤認する危険性があることを指摘する。この結果は、事故の原因となるスピードの出し過ぎが、スピードの誤認ではなくカーブの強さの誤認による可能性もあること、およびそれに対する新しい注意喚起の方法が考えられることを示唆するものである。
- 有向辺の追加に伴うグラフラプラシアンの固有値の増減 / ○本田 悠希 (近畿大学), 中島 弘之 (近畿大学) [概要]
マルチエージェントシステムの合意制御において,
ネットワーク構造を表わすグラフのラプラシアンが
重要な役割を果たす.特に,ラプラシアンの第2固有値
(実部が2番目に小さい固有値)が合意速度を決定するが,
有向グラフの場合にはその性質はあまり研究されていない.
本報告では,有向辺の追加に伴う第2固有値の増減について,
有向木グラフを対象として考察し,無向グラフとは異なって,
固有値が減少する場合のあることを示す.
- 解析的に求解可能な円筒領域における弾性体の振動固有値問題について / ○山田 貴博 (横浜国立大学) [概要]
本研究では,数値解の特性評価を目的として,弾性体の振動固有値問題において,陽な形で厳密解を表すことが可能な問題を構成する.具体的には,円筒領域を設定し,滑り境界を設定することで,弾性波動の定在波として表される問題が得られる.
▷ [研究部会OS] 応用可積分系(3) [9月9日:13:20-14:40:D]
- 負の結合定数を持つ蔵本モデルでの同期現象に現れる多様な平衡状態 / ○蜂須賀 秋人 (宇都宮大学大学院工学研究科情報システム科学専攻), 小池 正史 (宇都宮大学学術院), 矢嶋 徹 (宇都宮大学学術院) [概要]
蔵本モデルは,振動子集団の同期現象を記述する.振動位相の時間発展は他振動子との位相差に依存する.正の結合定数は位相差を小さくし,集団的同期に導く.
本研究は負の結合定数の場合を分析する.正方格子上では位相差は成長し,平面上の隣接振動子は逆位相に同期する.境界条件と両立しない場合は同期状態にも変化が見られ,不安定な同期も存在する.境界条件・初期条件により終状態を分類し,報告する.
- 双安定性を示すある非線形差分方程式の交通流モデルとしての妥当性 / ○岡本 和也 (武蔵野大学大学院 工学研究科 数理工学専攻), 友枝 明保 (武蔵野大学 工学部 数理工学科) [概要]
交通流モデルの一つの最適速度モデルは双安定構造を持つことが知られている.双安定構造とは,ある密度領域において二つの安定な状態を示す性質であり,交通流モデルにおいて非常に重要であることが知られている.本講演では,交通流数理モデルと解釈しうるある非線形差分方程式においてこの双安定性を示す解が数値的に得られたことなどの数値実験結果について発表する.
- Newell-Whithamモデルの厳密解の解析 / ○臼見 太佑 (法政大学大学院理工学研究科), 礒島 伸 (法政大学理工学部) [概要]
鈴木らによる先行研究で, 遅延微分方程式Newell-Whitham(NW)モデルと可積分であるLotka-Volterra方程式(Kac-van Moerbeke系)との対比に注目した, NWモデルの時間差分化が提出済みである. 本研究では, 先行研究で提案されたNWモデルの厳密解である孤立波解, 衝撃波解, およびこれらに摂動を加えた場合について解析を行い, その結果について報告する.
▷ [正会員OS] 位相的データ解析(3) [9月9日:13:20-14:40:E]
- 位相的データ解析による非晶質材料の構造研究 / ○小野寺 陽平 (京都大学), 小原 真司 (物質・材料研究機構), 田原 周太 (琉球大学), 増野 敦信 (弘前大学), 井上 博之 (東京大学), 志賀 元紀 (岐阜大学), 平田 秋彦 (早稲田大学), 土谷 浩一 (物質・材料研究機構), 平岡 裕章 (京都大学), 大林 一平 (理化学研究所), 尾原 幸治 (高輝度光科学研究センター), 水野 章敏 (函館工業高等専門学校), 坂田 修身 (物質・材料研究機構) [概要]
原子配列に長周期的な秩序を持たないガラス・液体・アモルファスといった非晶質材料について、量子ビーム実験と理論計算、計算機によるモデリングを駆使して3次元構造モデルを構築し、パーシステントホモロジー解析を中心とした位相的データ解析を適用した。講演では解析によって得られた”乱れた原子配列の中に潜んでいた構造秩序”について報告する。
- サッカーのトラッキングデータに対する パーシステントホモロジーを用いた解析の試み / ○沼田 泰英 (信州大学理学部) [概要]
第9回スポーツデータ解析コンペティションでは, J1リーグ戦2018年21節から25節の45試合のトラッキングデータ (各試合における各時刻での選手の位置情報) について解析を行った. このデータから, パーシステントホモロジーを用いることで, 各チームにおける各選手の役割についての情報が得られるか試みた. このとき行った解析方法の概略についてお話する.
- Mapperを用いた企業の技術戦略の位相的データ解析 / ○ESCOLAR Emerson Gaw (理化学研究所革新知能統合研究センター / 京都大学高等研究院), 平岡 裕章 (京都大学高等研究院), 伊神 満 (Yale Department of Economics), OZCAN Yasin (FTI Consulting) [概要]
企業の技術革新を位置付けるためには,まずは各企業を技術空間中にマッピングしたい.しかし技術空間は高次元であって,その構造を忠実に表現するのは難しい.そこで本研究では,Mapper解析を用いて技術空間を可視化する方法を提案する.解析過程で,フレアーと呼ぶ,企業の独自性に関係する構造を観察したため,検出するアルゴリズムを提案する.その結果,フレアーの長さは企業の業績指標と相関していることが分かった.
- Mapperに基づく遺伝子発現データの細胞分化構造解析 / ○井元 佑介 (京都大学高等研究院), 平岡 裕章 (京都大学高等研究院), 中村 友紀 (京都大学医学研究科), 小島 洋児 (京都大学iPS細胞研究所), 斎藤 通紀 (京都大学高等研究院) [概要]
Mapperはデータのクラスタリングに基いてデータのトポロジカルな構造をグラフで表現する位相的データ解析手法の一種であり、データサイズに対して計算コストが比較的低コストなので単一細胞遺伝子発現データのような高次元データに適している。本講演ではiPS細胞の分化誘導実験における単一細胞遺伝子発現データに対するMapperの適用事例を紹介し、細胞分化構造同定のためのMapperを応用した解析手法を提案する。
▷ [研究部会OS] 計算の品質(1) [9月10日:09:10-10:30:A]
- Navier-Stokes方程式の定常解の検証における若干の問題 / ○劉 雪峰 (新潟大学) [概要]
3次元領域におけるNavier-Stokes方程式の解の検証では、divergence-free条件を厳密に満たす有限要素空間とHypercircle法との組み合わせで、解の検証が可能となっています。ただし、divergence-free条件の処理に使用されるラグランジュの未定乗数法によって、関わる行列のサイズが実際の関数空間の次元の数倍になって、行列の条件数が大きいという問題があります。本発表では、解の検証計算に現れる行列の問題を説明して、取り込んでいる制約条件式のスケーリングなどの手法を説明します。
- 平面における曲線の位置関係の厳密計算法 / ○邵 文炳 (中国科学技術大学, D2), 劉 雪峰 (新潟大学), 陳 発来 (中国科学技術大学) [概要]
A robust and efficient algorithm is proposed to guarantee the intersection points of the algebraic curves within a specified area. In the proposed method, we utilize the fundamental methods in the field of Computer Aided Geometric Design (CAGD) and the field of solution verification for nonlinear equations.
For example, the Bernstein-Bézier representation of curves and the resultant computation of polynomials are used to fastly exclude that the region without intersection points and the Krawczyk method is used to find a sharp and guaranteed bound for the intersection point.
- Lagrange補間関数の最大値ノルム誤差評価 / ○Galindo Shirley Mae (Niigata University), Liu Xuefeng (Niigata University) [概要]
For the Lagrange interpolation operator, we consider bounding the maximum norm of interpolation error by using the H2 semi-norm of the given function. For a triangle element, we obtain explicit upper bound for the interpolation error constant. Also, from the analysis of the dependency of the constant on the shape of triangle, it is shown that the interpolation error constant diverges as the minimum inner angle of the triangle tends to zero.
▷ [正会員OS] 応用力学系(3) [9月10日:09:10-10:30:B]
- 摂動を受けるレイリー・ベナール対流に現れるラグランジュ・コヒーレント構造とローブダイナミクス / ○渡辺 昌仁 (早稲田大学大学院), 喜多村 友祐 (早稲田大学大学院), 八田 尚樹 (早稲田大学大学院), 鎌倉 良介 (早稲田大学大学院), 吉村 浩明 (早稲田大学) [概要]
定常なレイリー・ベナール対流の流れ場は,温度差の変化に伴って臨界レイリー数を超えると僅かに振動を起こすことが知られている.本講演では,このような摂動を受けるレイリー・ベナール対流に関する実験を実施し,粒子画像流速測定法による流速ベクトル場の計測を行い,データに基づいてラグランジュ・コヒーレント構造を抽出する.その上で,セル境界付近で安定・不安定多様体の絡まり合いによってローブが形成されることを示し,流体粒子のセル間の輸送構造を実験的に明らかにする.
- 気液混合体モデルによるクラウドキャビテーションの非定常挙動と渦流れ構造 / ○牛奥 隆博 (早稲田大学大学院), 吉村 浩明 (早稲田大学) [概要]
キャビテーションは,相変化に伴って発生する無数の微小な気泡が一塊のクラウドとして発生し,成長から圧壊まで集合的に振る舞う非定常現象として知られている.特に,圧壊によって衝撃波が発生するが,その発生メカニズムは十分に理解されていない.本講演では,水ジェットの噴射に伴うクラウドキャビテーションに注目して,気液混合体によるクラウドのモデル化を行い,ラグランジュ的な流れ場解析によってその非定常挙動と渦流れの関係を明らかにする.
- 吸引領域の形成過程から考える受動歩行におけるカオスアトラクタの消滅 / ○岡本 耕太 (京都大学), 青井 伸也 (京都大学), 大林 一平 (理化学研究所), 國府 寛司 (京都大学), 泉田 啓 (京都大学), 土屋 和雄 (京都大学) [概要]
受動歩行の吸引領域はフラクタル様になり,そのメカニズムはポアンカレ写像の逆像による引き伸ばしと折り畳みの作用によることを先行研究で明らかにした.一方で,受動歩行では,傾斜角をパラメータとした周期倍分岐を繰り返してカオスアトラクタになり,閾値を超えると突然消えることが知られている.この消滅は,カオスアトラクタが吸引領域の境界に衝突することで起こる境界クライシスより説明できるが,本研究では先行研究で明らかにした吸引領域の形成メカニズムに基づいて説明できることを述べる.
- バーチャルカンチレバーとバーチャルカップリングによる高感度微小質量計測 / ○藪野 浩司 (筑波大), 笠井 勇希 (筑波大), 山本 泰之 (産総研), 松本 壮平 (産総研) [概要]
複数の同一振動子を弱連成させることにより発生するモード局在化を利用した、高感度質量計測の研究が盛んにおこなわれている。超高感度化に向けて、同一のカンチレバーを作ることおよび超弱連成化が必要であるが、機械工作精度の限界から実現できない状況にある。この状況を打破するため、一部の振動子のダイナミクスと連成効果をコンピューター内で実現することを提案し、実験によってその有効性を検討する。
▷ [一般講演] 一般講演(5) [9月10日:09:10-10:30:C]
- 逆関数のTaylor展開式を利用した無限振動型関数の数値積分 / ○平山 弘 (神奈川工科大学) [概要]
逆関数を満たす常微分方程式を級数展開法で解くことによって、逆関数のTaylor展開式が得られる。これを無限区間振動型関数の積分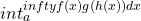 (g(x)は正弦関数などの振動型関数)で
(g(x)は正弦関数などの振動型関数)で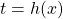 と置くと、単純な無限区間振動型関数
と置くと、単純な無限区間振動型関数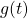 の積分になる。この積分を部分積分を繰り返す方法によって級数展開する。
その級数を計算することによって、効率的に計算出来る。
の積分になる。この積分を部分積分を繰り返す方法によって級数展開する。
その級数を計算することによって、効率的に計算出来る。
- 各点での直交性を持つHelmholtz-Hodge分解の構成について / ○須田 智晴 (慶応義塾大学) [概要]
Helmholtz-Hodge分解(HHD)とはベクトル場を勾配ベクトル場とソレノイダルベクトル場の和に書き表す分解である.特にこれらの成分が各点で直交性を持つHHDはLyapunov関数の構成に用いることができる.今回は線形系と平面系の場合についてそのようなHHDの構成法を述べるとともに,Lyapunov関数の別の構成法であるSDE分解についても紹介し,各点での直交性を持つHHDとの関係を述べる.
- 確率微分方程式に対する正値性保存スキームについて / 石渡 哲哉 (芝浦工業大学 システム理工学部 数理科学科), ○安孫子 啓介 (芝浦工業大学 大学院 システム理工学専攻) [概要]
本研究では, 一般的な確率微分方程式に対し, 伊藤の公式を用いた正値性保存スキームの構成方法を提案する. 変換後の方程式に対する離散近似は, Euler-Maruyamaスキームなどの既存のスキームを適用する. 実際の数値計算においては, 提案する手法による変換後の方程式に対する数値解を求め, その後, 逆変換をすることで元の方程式に対する数値解を得る.
- スプライン補間を用いた局所的陰関数曲面の生成 / ○工藤 雅也 (立命館大学大学院情報理工学研究科), 藤田 宜久 (立命館大学情報理工学部), 仲田 晋 (立命館大学情報理工学部) [概要]
本研究の目的は形状表面付近のみを必要な領域として構成する局所的陰関数曲面を滑らかに生成することである.先行研究では曲面にてエッジができるという課題があった.エッジができると本研究の使用用途である流体シミュレーションにおいて本来とは違う挙動をする可能性があるため,スプライン補間を用いて先行研究の課題を解決することを試みた.本研究の実現により滑らかさを考慮しつつ,高解像度でもデータ量の少ない陰関数曲面を生成可能になった.
▷ [研究部会OS] 数理設計(1) [9月10日:09:10-10:30:D]
- Bifurcation analysis for a two-phase overdetermined problem of Serrin type / ○Cavallina Lorenzo (東北大学大学院理学研究科), 谷地村 敏明 (京都大学高等研究院 ヒト生物学高等研究拠点) [概要]
We consider an overdetermined problem of Serrin-type with respect to an operator in divergence form with piecewise constant coefficients. We give conditions for unique local solvability near radially symmetric configurations by a perturbation argument relying on shape derivatives and the implicit function theorem. Moreover, by means of the Crandall-Rabinowitz theorem, we show that there exist infinitely many branches of symmetry-breaking solutions that bifurcate from radially symmetric configurations whenever the above-mentioned conditions are not met.
- Analysis on a two-phase geometric optimization problem / ○谷地村 敏明 (京都大学高等研究院), カヴァッリーナ ロレンツォ (東北大学大学院理学研究科) [概要]
本講演では,二つの物質からなる複合媒質のねじり剛性最大化問題に関連する形状最適化問題について考える.特に二相Serrin型優決定問題について考察し,Kohn-Vogelius汎関数とH^1勾配法を用いた数値アルゴリズムについて報告する.
- 複雑流体場における形状最適化 / ○中澤 嵩 (大阪大学MMDS) [概要]
本講演では,線形安定性解析で得られる最大固有値実部を目的関数とした形状最適化問題をNavier-Stokes問題に適用した結果を述べる。
- 領域変動型形状最適化問題における評価関数の2階形状微分について / ○畔上 秀幸 (名古屋大学) [概要]
領域変動型形状最適化問題において評価関数の2階形状微分の定義とその評価方法を見直す.1階形状微分は任意の領域変動に対する有界線形汎関数として定義される.2階形状微分は,1階形状微分の定義で使われた任意の領域変動とは別にあらたに任意の領域変動を仮定して,それに対する有界線形汎関数として定義される.その際,2番目の領域変動が1番目の領域変動に影響を与えないように定義を見直す必要があることを論ずる.
▷ [研究部会OS] 折紙工学(1) [9月10日:09:10-10:30:E]
- 折紙工学援用による自動車クラッシュボックスの圧潰エネルギー吸収特性向上の検討 / ○楊 陽 (明治大学), 趙 希禄 (埼玉工業大学), 萩原 一郎 (明治大学) [概要]
乗員の安全保護のため、車両前部の左右に配置されるクラッシュボックスにできるだけ多く圧潰エネルギーを吸収させることは非常に重要である。
折紙工学の研究成果から側面壁に適当に折り線を入れることによって圧潰長さは構造全長の90%以上続けられる特性を得ているので、一般的な横断面構成、軸方向の段差付きの新型クラッシュボックスの開発を図る。クラッシュボックス構造を分析し、パラメータ変化により吸収エネルギー最大を目的とする解析について検討を行う。
- トラスコアパネルの衝撃エネルギ吸収特性と座屈形状の関係 / 石田 祥子 (明治大学), ○浅上 隆登 (明治大学) [概要]
自動車の衝撃試験において、衝撃エネルギ吸収の性能要件を満たす軽量構造の開発が進んでおり、その1つにトラスコアパネル(TCP)がある。TCPに時速60kmで錘を衝突させる動的数値解析を行い、TCPのエネルギ吸収量や座屈形状との関係を明らかにすることが本研究の目的である。コア形状が異なる6種類のTCPを用いて解析を行った結果、コア側面とコア底面との角度が鋭角となる設計において、錘とコア上面との接触面積が増えて錘の荷重に耐えることができ、コア側面が外側に座屈しにくく、エネルギ吸収量は大きくなることが明らかになった。
- 空間充填構造の一考察 / ○佐々木 淑恵 (明治大学), 楊陽 (明治大学), 萩原 一郎 (明治大学) [概要]
正四面体と正四面体の組合せは空間充填ではないが横から見ると充填されており動かない。
この構造と正四面体と正八面体ハーフとの組合せの空間充填構造と特性がどのように異なる
かを、固有周波数と3点曲げ強度から明らかにする
- 有限要素法を用いたダイヤモンドシェルの折紙工学からのアプローチ/シミュレーションと実験との比較 / ○崎谷 明恵 (明治大学), 萩原 一郎 (明治大学), 橋爪 崇弘 (明星大学), 寺田 耕輔 (明星大学) [概要]
吉村パターンから着想を得て三浦公亮氏によってダイヤモンドシェル構造は生まれた。本研究は、この構造に注目し円筒型薄肉構造を研究することにより、これからの新しい構造に生かすことを目的とする。まずは有限要素法を用いたシミュレーションソフトウェアでダイヤモンドシェル構造を計算し、実際の実験との比較をし、考察する。
▷ [研究部会OS] 数理ファイナンス(1) [9月10日:09:10-10:30:F]
- Optimal investment-consumption-insurance with partial information / ○畑 宏明 (一橋大学大学院経営管理研究科) [概要]
本講演では、賃金労働者に対する最適な投資、消費、生命保険の購入問題を検討扱う。 線形Gauss型確率ファクターモデルを扱い、 賃金労働者がファクタ過程を観察できず、リスクのある資産の過去の情報のみを用いた部分的可観測な場合を扱う。 この問題を部分可観測確率的制御問題として定式化し、 動的計画法の原理を適用して、ハミルトン-ヤコビ-ベルマン方程式と2つの後方確率微分方程式を導き、明示解を得ることによって解決する。
- An Insurance Risk Model with an Exponential Functional of Renewal-Reward Processes / ○今村 悠里 (金沢大学理工学域数物科学類) [概要]
本講演では自然災害によって被害を受けた住宅のローン支払いを免除する集団住宅ローン返済モデルとその破産確率を導入する。この研究は、地震などの自然災害によって家を失ったにも関わらず、住宅ローンを支払い続けなければならず、また新規住宅購入に対する住宅ローンも払うことになる二重債務問題が動機となっている。モデルとしてリニューアル・リワード過程の指数汎関数を用いる。有限満期保険の生存確率の漸近挙動が指数的減少であることを示し、また無限満期保険の生存確率との比較を行う。
本研究は赤堀次郎氏、Corina Constantinescu氏, Hai Ha Pham氏との共同研究である。
- CIR 強度をもつ多変数ホークス過程のシミュレーション方法 / 安田 和弘 (法政大学), ○吉田 賢樹 (法政大学大学院理工学研究科システム理工学専攻) [概要]
Dassios, et al. (2017) において,CIR 強度をもつホークス過程のシミュレーションアルゴリズムが提案された.そのなかで,CIR 強度をもつ多変数ホークス過程のアルゴリズムについて述べられているが,実際シミュレーションを行うと理論値との誤差が大きく,そしてアルゴリズムの理論的背景にも問題があると思われる.そこで,理論的背景からアルゴリズムを考え直し,その後シミュレーション結果と理論値を比較することで再構築したアルゴリズムを検証する.
- 情報アプローチによる信用リスクの伝播 / 中川 秀敏 (一橋大学国際企業戦略研究科), ○高田 英行 (東邦大学理学部) [概要]
信用リスクの伝播メカニズムの把握は、ポートフォリオ単位でのリスク評価やカウンターパーティリスク評価において重要である。本研究では、Brody-Hughston-Macrina(2010)が単一企業に対して提唱した「情報アプローチ」モデルを、複数企業に適用できるよう拡張することで「情報」という視点での伝播メカニズムのモデル化を試みる。特に、2企業の場合における割引債価格の挙動を明らかにする。
▷ [研究部会OS] 計算の品質(2) [9月10日:10:40-12:00:A]
- 非線形シュレディンガー方程式の厳密な数値求積法 / ○高安 亮紀 (筑波大学) [概要]
本講演では、周期境界条件下の2次の非線形項を持つシュレディンガー方程式の初期値境界値問題を考え、時間変数にチェビシェフ級数、空間変数にフーリエ級数を用いるスペクトル法によって得られた近似解の近傍に真の解の時間局所包含を精度保証付き数値計算で得る方法を紹介する。本手法の特徴として、近似解での線形化問題の解作用素を用いる不動点形式を利用する事で、数理解析で用いるストリッカーツ評価の縮小性を利用しない点を強調したい。
- チェビシェフ級数を用いた逐次連立による非線形常微分方程式系の初期値問題の精度保証付き数値解法 / ○舩越 康太 (筑波大学大学院システム情報工学研究科リスク工学専攻), 高安 亮紀 (筑波大学システム情報系) [概要]
本講演では、チェビシェフ級数を用いた常微分方程式系の初期値問題に対する精度保証付き数値計算手法を紹介する。
問題を一定の時間幅毎に区切り、不動点写像を定義し、縮小性を示すことで解の精度保証付き数値計算を実行する。縮小性を示す際にRadii Polynomialsの逐次連立を行うことで、解区間の増大を抑える。
本手法と既存手法との比較から本手法の特長と今後の課題を述べる。
- 精度保証付き数値計算を用いたHenon方程式の多重解の存在証明 / ○浅井 大晴 (早稲田大学大学院 基幹理工学研究科 数学応用数理専攻), 田中 一成 (早稲田大学 理工学術院総合研究所 数理科学研究所), 大石 進一 (早稲田大学 理工学術院) [概要]
Henon方程式はパラメータ値を固定した場合でも複数の解を持ち、対称な凸領域上であってもその中心について非対称な解を持つと予想されている。それら多重解が真に存在する事を精度保証付き数値計算を用いて計算機援用証明した結果を報告する。加えて線対称性やピークの値による解の分類も行う。
- 任意三角形領域の精度保証付き数値2重積分における領域分割を用いた高精度化の研究 / ○田中 佑奈 (早稲田大学), 小林 領 (帝京平成大学), 大石 進一 (早稲田大学) [概要]
精度保証付き数値2重積分では、任意の三角形領域に対する剰余項の計算で複数の高階微分が現れて精度が悪くなる。Duffy変換などで三角形領域を長方形領域に変換することで高階微分の計算回数を削減できる。但し、長方形を均等に分割すると元の三角形における分割領域の大きさに偏りが生じる。
この偏りを減らすために分割領域ごとのヤコビアンの最大と最小の比を考慮した3つの四角形に分割する高精度な方法を提案する。
▷ [正会員OS] 離散数理モデルの諸相(1) [9月10日:10:40-12:00:B]
- ファジー化に適したセルオートマトンの表現とその応用 / ○渡邉 扇之介 (福知山公立大学), 西田 優樹 (同志社大学), 福田 亜希子 (芝浦工業大学), 渡邊 芳英 (同志社大学) [概要]
セルオートマトン(CA)のファジー化とは従来,変数の値が0または1の2値を取るCAの多項式表現に対して,変数に閉区間[0,1]上の値を代入することを指す.本講演では,2値に限らない任意の離散値を取るCAのファジー化手法を提案する.また,ファジー化によって得られるCAをファジーセルオートマトン(FCA)といい,本講演では3値のFCAに着目し,その性質と応用を紹介する.
- ARデバイスによるセル・オートマトン遷移の可視化 / 中原 良真 (広島大学), コン ギルタク (広島大学), ○今井 克暢 (広島大学) [概要]
ライフゲームの種々の配置を設計する多数の試みが、その数理的な性質の解明にも大きく寄与したように、セルオートマトン(CA)の規則や配置の設計を支援するツールは重要である。3次元CAの研究が少ないのは設計に使えるシミュレータがほとんどないことも大きな要因である。本研究では、近年急速に発展しつつあるArgumented Reality (AR)デバイスによるCAの設計支援ツールのプロトタイプを示す。
- 二分木の枝分かれの定量化と漸近的な性質について / ○山本 健 (琉球大学理学部) [概要]
本講演では、木グラフ(主に二分木)の枝分かれの構造を特徴づける分岐比という量を導入し、その離散数学的および確率論的な研究の展開について概説します。具体的な計算例として,ランダム二分木および二分探索木を取り上げます。ただし、本セッションが広く離散数理モデルに関するものであることから、技術的な細部の説明は最小限にとどめ、研究の背景や問題意識を中心に紹介する予定です。
- 計算ホモロジーを用いた非晶質構造の局所秩序抽出 / ○平田 秋彦 (早稲田大学) [概要]
材料の物性・特性を理解するにはその材料の原子配列を明らかにすることが欠かせない。非晶質と呼ばれる材料は、結晶とは異なり原子配列に周期性が無く、その解明は非常に困難であり、この分野では挑戦的な課題となっている。本講演では、非晶質の構造モデルから如何にして隠れた秩序に関する情報を抽出するか、主に計算ホモロジーを応用したアプローチについて紹介する。
▷ [正会員OS] 多倍長精度浮動小数点演算の高速化手法と応用(1) [9月10日:10:40-12:00:C]
- 多倍長精度浮動小数点演算の素粒子物理学への応用 / ○石川 正 (高エネルギー加速器研究機構) [概要]
計算機の進展は、演算性能の向上は目覚ましいものがある。より速い計算できる環境が常に更新され、シミュレーションによる新しい世界を開拓している。現在、浮動小数点数表現を短くして、より大量な計算をするトレンドではあるが、逆に仮数部、指数部を長い表現する計算も高速化することができるようになり、素粒子物理学の理論計算が進展した。本口頭講演では素粒子物理学への応用を俯瞰する。
- AVX2を用いた高速な倍々精度疎行列計算ソフトウェアの有限要素解析への適用可能性評価 / ○菱沼 利彰 (株式会社科学計算総合研究所), 森田 直樹 (株式会社科学計算総合研究所) [概要]
高精度演算を用いれば反復解法の収束を改善できるが,高精度演算は計算に時間がかかる.
我々は高精度演算の実装手法の一つである倍々精度演算に着目し,CPU上でSIMD拡張命令AVX2を用いて疎行列やベクトルに対する計算を高速化してきた.
本発表では有限要素法ソフトウェアFrontISTRによる構造解析を対象として,構造解析に由来する疎行列に対する共役勾配法を高精度化する.収束改善効果や計算性能を元に提案手法の適用可能性を評価する.
- NVIDIA Volta GPU における浮動小数点演算を用いた剰余乗算の高速化 / ○杉﨑 行優 (筑波大学), 高橋 大介 (筑波大学) [概要]
本研究では剰余乗算を効率的に計算するモンゴメリ乗算アルゴリズムを NVIDIA Volta GPU 向けに実装し性能を評価した.本講演では,整数と浮動小数点の演算器が独立に存在し動作するという NVIDIA Volta GPU の特性を活かし,整数演算と浮動小数点演算の両方を用いてモンゴメリ乗算を計算した場合の性能の向上について報告する.
▷ [研究部会OS] 数理設計(2) [9月10日:10:40-12:00:D]
- 散乱行列と境界要素法に基づく周期散乱問題におけるトポロジー最適化 / ○松島 慶 (名古屋大学大学院), 飯盛 浩司 (名古屋大学大学院), 高橋 徹 (名古屋大学大学院), 松本 敏郎 (名古屋大学大学院) [概要]
本研究は散乱行列と境界要素法に基づく周期散乱問題における新たなトポロジー最適化法を提案する.提案手法は,まず散乱行列と円筒関数の格子和を用いることで,周期散乱を線形代数方程式に帰着させる.そして,この解に対するトポロジー導関数を新たに導出し,レベルセット法に基づくトポロジー最適化アルゴリズムに組み込む.本講演では提案手法を用いたトポロジー最適化の数値例を示し,その有用性を示す.
- 摩擦係数を最小とするテクスチャ形状に関する最適化および設計変数の更新式に関する考察 / ○笹岡 修太 (長岡技術科学大学), 倉橋 貴彦 (長岡技術科学大学) [概要]
摩擦面に加工されたテクスチャの形状は,摩擦係数に影響を及ぼす.本研究では,摩擦係数を最小とするテクスチャ形状の最適化と新たな設計変数の形状更新式を提案する.従来の最急降下法に基づく更新式を微分方程式に置き換え,テイラー展開を適応した.提案した更新式について,テクスチャの初期形状を変更し考察を行った.
- 弾性体の幾何学的非線形性を考慮した形状最適化 / 河合 竜雅 (長岡技術科学大学), ○片峯 英次 (岐阜工業高等専門学校) [概要]
幾何学的非線形性を考慮した弾性体に対して,剛性最大化を目的とした形状最適化問題を取り上げて,その解法を紹介する.平均コンプライアンス最小化の最適化問題を定式化し,随伴変数法を利用して形状更新の感度となる形状微分を導出した.導出した感度に基づいて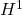 勾配法を適用し,FreeFEMを利用して解析した数値解析結果を紹介する.
勾配法を適用し,FreeFEMを利用して解析した数値解析結果を紹介する.
- 内部観測によるスカラー波動方程式のソース項同定問題に対するH1勾配法 / ○辻村 賢祐 (愛知県立大学大学院情報科学研究科), 代田 健二 (愛知県立大学情報科学部) [概要]
本研究では,スカラー波動方程式のソース項同定問題に対する数値的に安定な解法について考察する.観測データは内部観測で得られていると仮定し,そのデータを用いた汎関数を導入することで,元の問題を最小化問題へと帰着させる.最小化関数を得る方法としてH1勾配法を採用し,安定な数値解を得るためのアルゴリズムを導出する.数値実験により,導出アルゴリズムの妥当性を検証する.
▷ [研究部会OS] 折紙工学(2) [9月10日:10:40-12:00:E]
- 外周部の順序が与えられた地図折り問題の解法 / ○Jia Yiyang (筑波大学), 三谷 純 (筑波大学), 上原 隆平 (北陸先端科学技術大学院大学) [概要]
m×nの正方格子パターンを格子の辺に沿って折りたたむ問題を地図折り問題と呼ぶ。本発表では、外周に接する正方形のみの重なり順序が与えられた場合に、そのような順序を満たす折りたたみ状態を単純折りによって実現できるか判定する問題の解法を示す。部分的に順序が指定された判定問題はNP困難である場合が多いが、この問題は線形時間で解けることを示す。
- ホール問題における局所的に平坦折り可能な条件を満たす展開図の列挙と折り紙テセレーションへの応用 / ○中里 陸 (筑波大学), 三谷 純 (筑波大学) [概要]
折り紙設計におけるホール問題とは、展開図上で折り線の配置が定まっていない領域に、適切な折り線の配置を求める問題である。この解を生成するアルゴリズムが既に知られているが、得られた折り線が自己交差せずに平坦折りできることは保証されていない。そこで本研究では、既存のアルゴリズムに局所的に平坦折り可能な山谷割り当てを持つ展開図を出力する機能を追加した。また、ホール問題を応用した折り紙テセレーションの作成を行なった。
- 等面四面体を中心とした共通展開図問題の研究 / ○鎌田 斗南 (北陸先端科学技術大学院大学), 上原 隆平 (北陸先端科学技術大学院大学) [概要]
展開図とは、多面体の表面を(辺に限らずに)切り開いて得られる多角形のことである。2つの多面体A,Bに対して、A,Bが共通の展開図を持つかを決定することは重要な問題である。この問題は共通展開図問題と呼ばれ、A,Bが共に正多面体の場合が有名な未解決問題として知られている。本研究では、Aが等面四面体、Bが正多角柱、正多角錐、正多角形二面体などの場合について共通展開図が存在することを構成的に示す。
- 三角形メッシュモデルの折紙化手法における展開図の簡略化 / ○加藤 優弥 (筑波大学), 三谷 純 (筑波大学) [概要]
Origamizerは折りあげると目的の形状になるような展開図を生成できる代表的なソフトウェアであるが、得られる展開図は折線の数が多く、実際に折るのは多大な苦労を要する。
本研究では、素材によっては目的の形状が正確に作成できなくとも多少のズレなら許容できるとして、折線の除去や展開図の構造の変更、目的の形状の簡略化を行う。
▷ [研究部会OS] 数理ファイナンス(2) [9月10日:10:40-12:00:F]
- Queue-Reactive Hawkes過程を用いた注文発生と待ち注文数量がその後の注文発生強度に与える影響の分析 / ○野原 眞 (三菱UFGトラスト投資工学研究所), 中川 秀敏 (一橋大学大学院経営管理研究科) [概要]
本研究では、本邦株式市場の特定の銘柄における板情報から複数の注文を抽出し、最良気配値における指値注文量と注文の発生との関係について、Wu et al.(2019)が導入したQueue-Reactive Hawkes過程を用いて分析した。
主な結果として、仲値の変化は最良気配値における指値注文量の厚みに大きく依存しており、仲値が上昇(下落)した直後の最良売り(買い)気配値における指値注文量が極端に厚くなければ、さらに仲値が上昇(下落)しやすくなること、などが確認された。
- マクロ経済変数を含んだINARモデルによる倒産リスク伝播構造の推定とストレステストへの応用 / ○監物 輝夫 (一橋大学大学院経営管理研究科 博士課程) [概要]
Hawkes過程を用いたイベント発生のモデル化はファイナンス分野でも近年注目されている。
本研究では、日本における比較的長期の倒産履歴データを対象に、業種に基づいて複数のイベントタイプに分類し、そのうえで多次元Hawkes過程を用いて倒産発生の伝播構造をモデル化する。多次元Hawkes過程に付随する強度過程を特徴づける手法として、マクロ経済指標をINARモデルに組み込み、業種間での倒産発生の伝播構造を比較し、マクロ経済指標を含んだINARモデルによる依存関係のモデル化が、倒産過程の推定でマクロ経済指標を含まないモデルよりも優れていることを示すほか、ストレステストへの応用事例も併せて例示することで、実務の観点からもモデルの有効性を示す。
- 最小二乗確率的分類器による信用格付判別 / 斉藤 美穂 (青山学院大学大学院理工学研究科), ○山中 卓 (青山学院大学理工学部) [概要]
金融分野において機械学習手法を用いて企業の信用リスクを評価する試みがなされてきた.本発表では,最小二乗確率的分類器と呼ばれる機械学習手法を用いて,財務情報から企業の信用格付判別を行った分析例を報告する.
- モバイルデータの活用による経済指標の予測について / ○金子 拓也 (国際基督教大学) [概要]
本報告では、各種モバイルデータを活用した経済指標予測の試みについて紹介する。
▷ [研究部会OS] 計算の品質(3) [9月10日:13:20-14:40:A]
- Hilbert空間における線形作用素に対する可逆性検証の効率化 / ○渡部 善隆 (九州大学), 木下 武彦 (九州大学), 中尾 充宏 (早稲田大学) [概要]
一般のHilbert空間における線形作用素の可逆性を効率よく判定する精度保証付き検証アルゴリズムを2種類提案し、それらのアルゴリズムの応用として逆作用素の作用素ノルム評価を改善する手法について述べる。また、具体的な検証例として、2階楕円型作用素および重調和作用素を取り上げ、効率化を確認する。
- 楕円型境界値問題に対する解符号の事後検証法 / ○田中 一成 (早稲田大学), 浅井 大晴 (早稲田大学) [概要]
本講演では楕円型境界値問題を対象とし、あるノルムの意味で包含された解の符号の事後検証法を提案する。主に解の正値性の検証を行う理論と、それをもとに設計した数値アルゴリズム、およびプログラムの実装例を紹介する。同時に符号変化解への応用例を報告する。
- 半線形楕円型偏微分方程式の解の局所非存在証明法 / ○関根 晃太 (東洋大学), 中尾 充宏 (早稲田大学), 大石 進一 (早稲田大学) [概要]
楕円型偏微分方程式の境界値問題の解が閉球B内に存在することを,計算機を用いて証明する方法は,1988年に第二著者により考案され,それ以降の研究も広く知れ渡っている.
それに対し,本講演では,楕円型偏微分方程式の境界値問題に対し「解が閉球B内に存在しないこと」を計算機を用いて証明する手法を紹介する.
▷ [正会員OS] 離散数理モデルの諸相(2) [9月10日:13:20-14:40:B]
- 1次元格子上の量子ウォークを用いた量子テレポーテーションの研究 / ○山上 智輝 (横浜国立大学大学院理工学府数物・電子情報系理工学専攻), 瀬川 悦生 (横浜国立大学大学院環境情報研究院), 今野 紀雄 (横浜国立大学大学院工学研究院) [概要]
量子テレポーテーションとは,ある量子状態の伝送を行うプロトコルで,量子コンピュータの原理を用いた最も簡単なモデルの一つとして研究されている.一方,量子ウォークとは,量子情報科学の分野における注目を端緒に,近年その数学的構造(特に線型的拡がりや局在化),或いは実装の側面から幅広い応用が期待されている分野である.本研究ではそうした応用の1つとして量子テレポーテーションを取り上げ,その一般化を試みる.
- グラフクラスの有限性と禁止部分グラフ条件 / ○古谷 倫貴 (北里大学), 江川 嘉美 (東京理科大学) [概要]
本講演では,禁止グラフの三つ組条件のうち,それを満たす最小次数が3以上のグラフが有限種類しか存在しないようなものについて着目し,その特徴付けを目指した最新の成果を紹介する.また,その結果を用いたグラフ彩色アルゴリズムについても紹介する予定である.
- Max-plus行列の固有値・固有ベクトルとその拡張 / ○西田 優樹 (同志社大学大学院理工学研究科), 渡邉 扇之介 (福知山公立大学情報学部), 渡邊 芳英 (同志社大学理工学部) [概要]
Max-plus代数とは,加法として2数の最大値をとる演算,乗法として2数の和をとる演算をもつ半環である.Max-plus行列の固有値および固有ベクトルはグラフの閉路と深く関係することが知られている.また,行列の固有値は固有多項式の根となっているが,その逆は一般には成り立たない.本講演では,固有多項式の根に対してそれらに付随するベクトルを定義することで,固有値・固有ベクトルの概念を拡張する.
- クリティカルチェーン法における厳密最適解 ~Max-plus線形表現を用いたアプローチ~ / ○五島 洋行 (法政大学) [概要]
クリティカルチェーン法と呼ばれる,資源制約付きプロジェクトスケジューリング問題に対する厳密解法を与える。タスクの開始および終了時刻をmax-plus代数系での線形方程式系で記述し,タスクの実行時間と実行順序を所与とし,割当資源の組合せに対するメイクスパン最小化問題として定式化する。構築した手法を用いると,タスク数が20程度までのプロジェクトに対する厳密解が数十分以内に求められる。
▷ [正会員OS] 多倍長精度浮動小数点演算の高速化手法と応用(2) [9月10日:13:20-14:40:C]
- 3倍精度演算を用いた高速行列乗算 / ○幸谷 智紀 (静岡理工科大学) [概要]
3倍精度,即ちTD精度(Triple-double, TD)はFabianoらが提唱したTriple word演算に基づく実装で,無誤差変換技法を使用するDD精度(Double-double)とQD精度(Quad-double)の中間の桁数をサポートするマルチコンポーネント方式の多倍長精度演算である。本講演ではこのTD精度を用いた高速行列乗算が,誤差でも計算速度でもDD精度とQD精度の中間に位置し,この2つの精度を補完するものとして有効に活用できることを報告する。
- 尾崎スキームを用いたbinary128による4倍精度行列積 / ○椋木 大地 (理化学研究所), 尾崎 克久 (芝浦工業大学), 荻田 武史 (東京女子大学) [概要]
IEEE 754-2008 binary128は現時点でx86にハードウェア実装されていないが,GCC Quad-Precision Math Library(libquadmath)によりソフトウェア実装を利用できる.我々はこれと高精度行列積手法の尾崎スキームを用いて,入出力形式がbinary128の行列積をx86に実装した.演算の大部分はbinary64行列積(DGEMM)で計算でき,MPLAPACKのbinary128およびdouble-doubleの行列積よりも高い性能が得られた.
▷ [研究部会OS] 数理設計(3) [9月10日:13:20-14:40:D]
- 線形弾性波動方程式の係数同定問題に対するH1型解法 / ○OZTURK AHMET FURKAN (愛知県立大学 代田研究室) [概要]
本研究では,線形弾性波動方程式のラメ係数同定問題に対する数値的に安定な解法について考察する.
観測データは内部観測で得られていると仮定し,そのデータを用いた汎関数を導入することで,
元の問題を最小化問題へと帰着させる.最小化関数を得る方法としてH2勾配法を採用し,
安定な数値解を得るためのアルゴリズムを導出する.数値実験により,導出アルゴリズムの妥当性を検証する.
- 超弾性体の泳ぎ運動に関わるパラメータ同定と形状最適化 / ○林 拓也 (名古屋大学), 畔上 秀幸 (名古屋大学) [概要]
周期的な物体力を受けたとき超弾性体の運動が泳ぎ運動に近づくために影響のあるパラメータを同定する.その上で,形状最適化問題を再構築し,数値例を通して,超弾性体の振動モードを利用した泳ぎ運動創成に関する可能性を示す.
- 流れの最適制御のための強化学習 / ○清水 雅樹 (大阪大学大学院基礎工学研究科), 久保 晃 (大阪大学大学院基礎工学研究科), 成川 航祐 (大阪大学大学院基礎工学研究科) [概要]
流体中の物体運動の最適制御に関した強化学習のアルゴリズムについて報告する。有限自由度の流れの観測量と制御パラメータの関数として行動価値関数を推定することで、効率的な制御の最適化が可能であることを示す。
- 流体機械設計のためのベイズ最適化 / ○下山 幸治 (東北大学) [概要]
最適解を探索する過程の中で、様々な解に対して目的関数・制約条件関数を評価・比較する必要がある。実世界の設計問題で見られるように、大規模数値シミュレーションによって関数評価を行う場合、最適化計算全体に要する時間が膨大となる。本発表では、実設計最適化問題の高速解法に有効な「ベイズ最適化」の基礎を解説するとともに、流体機械設計への応用事例を紹介する。
▷ [研究部会OS] 折紙工学(3) [9月10日:13:20-14:40:E]
- 三次元モデルによる日本古来の扇の視覚効果の検証 / ○山崎 桂子 (明治大学), 阿部 富士子 (明治大学), 萩原 一郎 (明治大学) [概要]
和紙を折り竹串を刺して仕立てる日本の扇は三次元の芸術品である.扇の表面画像は,仕立て後の三次元形状を見越して二次元に描画されなくてはならないが,江戸時代の絵師たちのその技法は現代には残されていない.この技術を解明するため、筆者らは近似式を用いたデジタルの扇モデルを導出しているが、本研究ではこのモデルを用いて,表面画像の配置や扇のパラメータを変更することによる視覚効果を検証する.
- 有限要素法による垂直入射遮音特性シミュレーション技術の開発と折紙コアへの応用 / 阿部 綾 (明治大学), 屋代 春樹 (明治大学), ○萩原 一郎 (明治大学) [概要]
従来の遮音特性評価法には有限要素法で任意位置での音圧値を容易に求められる利点を活かし,定義に従って全ての節点での音圧から音響エネルギー密度を求め透過損失を算出することがあるが,これに対し,透過損失の算出に実験との対比をより容易とする効果的な代表節点の位置を絞り込む手法が提案されている.本報ではこれを基に,より正確な垂直入射遮音特性シミュレーション技術について論じ,折紙コアへの適用を図る.
- アルキメデス螺旋格子のボロノイ領域の面積の収束 / ○山岸 義和 (龍谷大学), 須志田 隆道 (サレジオ高専), Sadoc Jean-Francois (Univ Paris-Sud) [概要]
一般アルキメデス螺旋格子の上のボロノイ分割は、葉序螺旋の幾何学モデルの一つである。回転角の連分数展開の部分商が有界であると仮定して、一般アルキメデス螺旋の指数が1/2のとき(フェルマー螺旋)、ボロノイ領域の面積は、一つの値(円周率)に収束する。指数が1/2より大きいとき面積は無限大に発散し、1/2より小さいときは0に収束するが、その漸近挙動は一般アルキメデス螺旋の指数で記述される。
- 正二十四胞体からできる多重正八面体 / ○奈良 知惠 (明治大学), 伊藤 仁一 (椙山女学園大学) [概要]
正八面体の表面は,一組の平行な三角形面を互いに重なるように,平行なまま回転させて動かし,同時に他の6個の三角形面をうまい折り目で折っていくと,連続的に多重三角形に平坦化できる。それを利用すると,24個の正八面体から構成される4次元の正二十四胞体について,その三角形面全体からなる2-スケルトンを連続的に折り畳んで,多重正八面体に変形できる。ここでは,ジタ-(オクタ)バグの動きと関連させながら述べる。
▷ [研究部会OS] 数理ファイナンス(3) [9月10日:13:20-14:40:F]
- 時間変更を用いた1次元確率微分方程式の離散近似]{時間変更を用いた1次元確率微分方程式の離散近似の強収束について / 深澤 正彰 (大阪大学), ○池田 光優 (大阪大学) [概要]
本講演では,1次元確率微分方程式(SDE)の新たな数値計算法を提案する.本研究における手法は,DoeblinによるSDEの解の表現に基づいており.離散化したBrown運動の時間パラメータを常微分方程式によって時間変更することで真の解を近似することを目標とする.本研究の主な結果は,0<β<1/2について拡散係数がβ-Hölder連続のときにおけるSDEの弱解への強収束のレートを計算したことである.
- 多次元確率微分方程式の対称化における境界の曲面への拡張 / ○田村 勇真 (立命館大学大学院) [概要]
確率微分方程式の対称化は,barrier option の価格の計算法として2012年に今村氏らによって導入された手法であり,2014年には同氏らによって多次元の確率微分方程式にも拡張され,さらに2019年には菱田氏らが境界を曲面に拡張する予想を提示した.本講演では,菱田氏らの予想の証明に向けてこれまでに得られた結果を紹介する.
- ある確率微分方程式の解の局所密度関数のヘルダー連続性について / ○秋山 壮太 (芝浦工業大学 大学院 理工学研究科) [概要]
あるコンパクト集合上でのみ確率密度関数が見つかることがある. これを局所密度関数と定義する. ある条件を満たす係数をもつ確率微分方程式の解が局所密度関数をもち, さらにその局所密度関数がヘルダー連続性を持つことが(林・コハツヒガ・結城, 2013)によって示されている. 今回は, この結果を一般化した結果を紹介する.
- Stochastic delay equationに対する伊藤Taylor展開 / ○中津 智則 (芝浦工業大学数理科学科) [概要]
マルコフ型の確率微分方程式(Stochastic differential equation)に対し、伊藤の公式を繰り返し適用することで伊藤Taylor展開が得られることが知られている(e.g. Kloeden and Platen)。本講演では、係数が時間の遅れに依存するStochastic delay equationに対する伊藤の公式と伊藤Taylor展開に関する結果を紹介する。
▷ [研究部会OS] 計算の品質(4) [9月10日:14:50-16:10:A]
- GPUの単精度演算・Tensorコアを用いた行列積のエラーフリー変換 / ○尾崎 克久 (芝浦工業大学), 椋木 大地 (理研R-CCS), 荻田 武史 (東京女子大学) [概要]
本報告では,GPUの単精度演算およびTensorコアを用いた行列積のエラーフリー変換について述べる.行列積のエラーフリー変換は,浮動小数点演算を用いて行列積を行列の和に無誤差で変換する技術である.成分がある精度の浮動小数点数である行列の積を,その精度より低い精度の演算を活用して行列の和に変換する方法を述べる.単精度演算が倍精度演算の数十倍高速なGPUがあり,本研究ではこのような数値計算環境の活用を想定する.最後にTensorコアを用いた高速化についても述べる.
- 疎な係数行列を持つ最小二乗問題の精度保証付き数値計算法とその応用 / ○南畑 淳史 (中央大学), 荻田 武史 (東京女子大学), 大石 進一 (早稲田大学) [概要]
本発表では疎な係数行列を持つ最小二乗問題に対しLU分解を用いた精度保証付き数値計算法を提案する。最小二乗問題の精度保証付き数値計算法は一般的にはQR分解を用いた方法が用いられる。また、正規方程式を経由した場合はコレスキー分解を用いた方法を用いることができるが、条件数が問題となる。本発表ではコレスキー分解を用いた方法では難しい問題、QR分解を用いた方法では難しい大規模な問題などで提案手法が有効なことがあることを示す。
- 総和が最大となるベクトルを特定する精度保証付き数値計算法 / ○内野 佑基 (芝浦工業大学大学院理工学研究科), 尾崎 克久 (芝浦工業大学システム理工学部) [概要]
成分が浮動小数点数であるベクトルが複数ある中で,成分の総和が最大となるベクトルを特定する数値計算法を提案する.数値計算には丸め誤差が伴うため,計算して得られた総和の単純な比較では正確に特定できる保証はない.本研究では,フィルタリングとエラーフリー変換により,ベクトルの保存順序に効率が依存しない数値計算法を提案し,数値実験によりその有効性を示す.また,発表時にオーバーフローなどの例外への対処法も紹介する.
▷ [正会員OS] 時間遅れと数理(1) [9月10日:14:50-16:10:B]
- 階段形の非線形関数をもつ遅延微分方程式について / ○中田 行彦 (青山学院大学), Vas Gabriella (University of Szeged) [概要]
時間遅れのフィードバックを特徴付ける関数が適当な奇関数のとき、分布型の時間遅れをもつ微分方程式は最小周期が2となる周期解をもつ例が示されてきた。そのような周期解の安定性や分岐(またそれから発生する複雑な解挙動)は未解決な課題である。定数の時間遅れをもつ微分方程式に対して、(解挙動の計算が容易となるように)フィードバック関数を符号関数にした場合の、解の動態が調べられてきた。そのアイデアを利用して、本発表では、フィードバック関数を符号関数にした場合の、分布型の時間遅れをもつ微分方程式の解挙動について紹介する。適当な初期条件のもとで、解が最小周期2の周期解へと収束する結果を得たことを発表する。また任意の自然数kに対して、周期が 2/(2k+1) の周期解と、周期が 1/k の(広義な意味での)解が存在することを示す。
- 時間遅れを考慮に入れたBurgers方程式の大域解について / ○久保 隆徹 (お茶の水女子大学), 上田 好寛 (神戸大学) [概要]
交通流の数理モデルの1つとしてBurgers方程式がよく知られている.本講演では,そのモデルに運転手の反応遅れを考慮に入れたBurgers方程式について考察を行い,得られた時間大域解の存在定理を紹介する.
- 時間遅れを用いた交通流の数理解析に向けて / 宇田 智紀 (東北大学 材料科学高等研究所), ○西口 純矢 (東北大学 材料科学高等研究所) [概要]
交通流の数理モデルには,マクロな視点による連続体モデルとミクロな視点による車両追従モデルが存在する.後者においては,個々のドライバーの反応による時間遅れを導入することがより現実的である.本講演では,時間遅れを持つ最も簡単な線型の車両追従モデルを考え,その一様流れ安定性の必要十分条件を導出する.
- 遅れ破産問題 / ○大平 徹 (名古屋大学・多元数理) [概要]
遅れとゆらぎをともに含むような系の研究の一つとして, 確率論の古典的問題である「破産問題」に遅れをとりいれた「遅れ破産問題」を提案し, その性質を考察した. ここで遅れとは, 賭けの勝敗から実際の資産の支払いや受け取りの間の時間であり, 給与の遅配,クレジットカードなどの支払いの猶予など, 現実の状況も反映している. この問題を制限付きランダムォークに遅れを導入することで記述・解析し, 破産確率についての近似式を得た.
▷ [正会員OS] 皮膚科学と数理科学の協働 [9月10日:14:50-16:10:C]
- 創傷治癒における皮膚幹細胞の寄与 / ○夏賀 健 (北海道大学病院皮膚科) [概要]
皮膚は生体の最外層を覆う最大の臓器であり、そのバリア機能によって体内からの水分の喪失を防ぐとともに、外来抗原から体内の臓器を保護している。皮膚の損傷は、バリア機能の喪失を意味しており、速やかな修復を必要とする。本講演では、外的刺激に対する皮膚幹細胞の応答について概説する。
- 皮膚バリア機能を有する表皮数理モデルとその応用 / ○大野 航太 (北海道大学), 小林 康明 (北海道大学), 長山 雅晴 (北海道大学) [概要]
皮膚の最も外側に位置する表皮はその大部分が角化細胞で構成されている.角化細胞は表皮の最下層で分裂を行い,分化しながら上層へと移動し,やがて表皮から剥離する.分化した細胞は層構造を作り,各層では生命維持のためのバリア機能が備わっているが,分裂と剥離を繰り返しながらもその構造を保つ.我々はこの様な表皮の特徴的な構造を再現する様な数理モデルを構築した.講演では応用として病態の再現に用いた例も紹介する.
- 基底膜上に形成されたピラー構造パターンによる表皮モデル角層バリア機能への影響 / ○熊本 淳一 (北海道大学), 藤本 興治 (大日本印刷株式会社), 長山 雅晴 (北海道大学), 傳田 光洋 (株式会社資生堂) [概要]
表皮モデルは皮膚疾患等の基礎研究にとって重要なリサーチツールである。本研究では、フォトリソグラフィーを用いて表皮モデル基底膜上に直径15、20、30、50µmのプラスチック製円柱状ピラーを形成して、表皮モデルを構築しピラーの効果を評価した。その結果、20µmのピラーを用いた場合、最も厚い表皮、角質層を持つ表皮モデルが構築され、これにより基底膜の構造パターンによって表皮モデルの重層化に影響を与えることが判明した。
- 真皮の塑性変形と形態形成の数理モデル構築 / ○小林 康明 (北海道大学), 安ヶ平 祐介 (北海道大学), 大野 航太 (北海道大学), 長山 雅晴 (北海道大学) [概要]
皮膚における真皮の凹凸の形成過程を記述する数理モデルとして,これまでに真皮・基底膜・基底層細胞を粒子で表すモデルを構築してきた.このモデルでは基底膜の構成粒子は弾性膜で表される.本講演では真皮における毛包形成などの塑性変形を伴う形態形成を記述するためのモデルの拡張の試みについて紹介する.
▷ [正会員OS] データ駆動型モデリングへの幾何学的力学・計算代数学的アプローチ [9月10日:14:50-16:10:D]
- あるクラスの非線形拘束を受ける非ホロノミック系とディラック構造 / ○吉村 浩明 (早稲田大学基幹理工学部) [概要]
力学に現れる非ホロノミックな拘束は,多くの場合,一般化速度に関する線形拘束として与えられる.そのような系はラグランジュ・ダランベール原理によってディラック系として定式化できるが,一般に,非線形拘束を有する非ホロノミック系ではディラック構造を見出すことは困難である.本発表では,熱力学的非線形拘束と呼ばれるあるクラスの非ホロノミック拘束を受ける力学系ではディラック構造が存在し,一般化されたラグランジュ・ダランベール原理による定式化が可能であることを示す.
- Modified formal variational structures for general differential equations / ○彭 林玉 (慶應義塾大学), 小幡 研治 (慶應義塾大学) [概要]
Variational structures are fundamental in mechanics and physics. Among the many important properties, in particular, they allow a systematical construction of conservation laws via the celebrated Noether’s theorem; they also provide great convenience for developing structure-preserving numerical methods. In many cases, however, a natural variational structure is lacking and the formal Lagrangian method was introduced. It is an extension of the self-adjointness for Euler–Lagrange equations to non-variational systems.
In this talk, we modify the formal Lagrangian method to cover a wider family of differential equations, e.g., Burgers’ equation, generalized Camassa–Holm equation, Euler equations and Navier–Stokes equations. Consequently, conservation laws of those systems can be computed through an extended Noether’s theorem and we believe that the modified formal Lagrangian method will shed new light on geometric integrators for general differential equations.
- 確率的パラメータ多様体とそのベイズ推定について / ○小松 瑞果 (神戸大学大学院システム情報学研究科) [概要]
状態空間モデルの未知パラメータ推定において,ベイズ統計的手法が広く用いられるが,モデルが多項式の場合,この方法では,モデルの代数的構造を見落とす可能性がある.実際,モデルと観測誤差がない理想的なデータが与えられた場合,データを生成するパラメータは,パラメータ空間上の代数多様体をなす.そこで,本講演では,データの観測誤差を反映した,代数多様体の確率的な扱いを提案し,実際にベイズ推定を行う.
- データ駆動型アプローチによる動的システムのモデリング / ○大森 敏明 (神戸大学) [概要]
近年,データ駆動型アプローチに基づいて,観測データの背後に潜在するダイナミクスの抽出を実現するための手法が注目を集めている.本発表では,部分的に観測されるデータから複雑な動的システムを推定するためのデータ駆動型モデリング手法に関して概説する.
▷ [一般講演] 一般講演(6) [9月10日:14:50-16:10:E]
- 自己交差する閉曲線の曲線短縮問題に現れる曲率の爆発現象に関する一考察 / ○穴田 浩一 (早稲田大学高等学院), 石渡 哲哉 (芝浦工業大学システム理工学部), 牛島 健夫 (東京理科大学理工学部) [概要]
曲線短縮問題に現れる曲率の爆発現象を考えると、その収縮速度に関する準線形偏微分方程式の爆発解の漸近挙動を考察することに帰着できる。加えて、自己交差する閉曲線の曲線短縮問題に対する方程式の爆発解は、TypeII爆発をすることが知られており、これまで様々な研究がなされている。ここでは、この問題について、曲線の動きと曲率の爆発現象との関連について考察を行う。
- 代用電荷法の最小二乗法と不変スキームについて / ○渡邊 紘一郎 (愛媛大学大学院理工学研究科), 岡野 大 (愛媛大学大学院理工学研究科) [概要]
代用電荷法はポテンシャル問題に適した数値解法である.
最小二乗法は代用電荷法を満たす未定係数決定方法の一つである.
近似解を構成する際の分点数を増やすことができるのが利点である.
また, 不変スキームは近似調和関数に数学的に良い性質を与え, その採用は必須である.
しかし, 単純な最小二乗法の採用では不変性は保たれない.
そこで, 両者の採用を両立させる方法を提案し, 数値実験例を示す.
- 二重周期的ポテンシャル流問題に対するWeierstrass楕円関数を用いた代用電荷法 / ○緒方 秀教 (電気通信大学) [概要]
本講演では、二重周期的二次元ポテンシャル流に対する、新しい代用電荷法による数値解法を提案する。この問題では、解が二重周期関数を含むため、従来の代用電荷法では近似解を求めるのが難しい。そこで、Weierstrass楕円関数を用いて周期的対数ポテンシャルを構成し、その一次結合により解を近似する方法を提案する。この方法は、従来の代用電荷法の利点である計算が簡便でかつ高精度であるという性質を受け継いで、さらに、二重周期関数を含む解をよく近似する。数値例によりこの方法の有効性が示される。
- Deterministic and Stochastic Models of Nonlocal Diffusion on Inhomogeneous Networks / ○Watanabe Itsuki (Waseda University) [概要]
We discuss the difference of two mathematical models of nonlocal diffusion; the deterministic and stochastic models. The deterministic model is given by some reaction- diffusion equation, and the stochastic model is given by a multi-dimensional jump Markov process. In this talk, we show two limit theorems. First, by the law of large numbers, we show that the difference between the deterministic and stochastic models converges to 0 in probability. Second, we consider the rescaled difference, and show it weakly converges to the Ornstein-Uhlenbeck process on the Skorokhod space.
▷ [研究部会OS] 数理ファイナンス(4) [9月10日:14:50-16:10:F]
- 離散版のクラーク公式の応用について / ○大熊 香里 (QUICK), 赤堀 次郎 (立命館大学), 古市 優衣 (立命館大学) [概要]
クラーク公式とはブラウン運動の汎関数の確率積分表示を与える公式である.その離散版は,離散近似の誤差評価を与えるほか,近年著しく発展している確率数値解析に対して広く応用をもつ.本講演では,新しい応用の可能性について報告する.
- 離散時間バリアオプションのデルタの近似 / ○井上 源太 (芝浦工業大学 大学院 理工学研究科 システム理工学専攻) [概要]
本講演では、Black-Scholesモデルにおいて、経路依存型のオプションである離散時間のバリアを持つ「ダウンアンドイン・コールオプション」について、その価格に対するデルタと呼ばれる株価の現在価格に関するリスクについて考察する。Black-Scholesモデルにおいて、離散バリアオプションの価格は、連続バリアオプションの価格を用いて近似できることが知られている(Broadie, Glasserman and Kou, 1997)。今回はその結果を基に得られるデルタの近似と数値計算結果を示す。
- デルタ関数を含む期待値のカーネル密度推定について / ○杉嶋 涼 (芝浦工業大学大学院理工学研究科) [概要]
デルタ関数を含む期待値は,数理ファイナンスでは金融商品のリスクとして現れる.本講演では,この期待値をカーネル密度推定を用いて推定する方法を紹介する.この方法は密度関数を推定するための通常のカーネル密度推定法を含み,その一般化となっている.また,推定に必要なバンド幅と呼ばれるパラメータの選び方についても併せて述べる.
- 時間非一様なMarkov過程の効率的サンプルパス生成とバリア・オプションのGreeks計算 / ○石谷 謙介 (東京都立大学) [概要]
講演では,停止時刻を含むようなWiener汎関数に対する超関数微分の計算方法と,その応用としてバリア・オプションのGreeksの準解析的計算方法を提案する.更に,この提案手法を用いてGreeksを計算するために必要となる,3次元Bessel橋,Brownian meanderやBrown引越過程といった時間非一様なMarkov過程の効率的サンプルパス生成方法についても紹介し,提案手法を用いてバリア・オプションのGreeksを高精度に計算できることを確認する.
▷ [正会員OS] FreeFEM の開発と利用 [9月10日:16:20-17:40:A]
- Web-based Interactive Visualization Interface for FreeFEM / ○Lee Yu Hsun (京大情報) [概要]
In this talk, we introduce an intuitive web interface for the visualization of numerical results calculated in FreeFEM. With our web-based interface, the user can easily access data interactivity and decide what to show on the figure on modern browsers like Edge, Safari, Chrome, etc. Also, users can interact with a live render animation for problems with time evolution. We include a lightweight HTTP (Hypertext Transfer Protocol) server package in our FreeFem dynamic loading module written in C++.
- Structural topology optimization of fluid-structure problem using adaptive mesh refinement based on the level-set method / ○Hao Li (Department of Mechanical Engineering and Science, Graduate School of Engineering, Kyoto University), Kazuhiro Izui (Department of Mechanical Engineering and Science, Graduate School of Engineering, Kyoto University), Shinji Nishiwaki (Department of Mechanical Engineering and Science, Graduate School of Engineering, Kyoto University), Takayuki Yamada (Department of Strategic Studies, Institute of Engineering Innovation, The University of Tokyo), Pierre Jolivet (Institut de Recherche en Informatique de Toulouse, France) [概要]
We propose a parallel distributed and open-source framework for full-scale 3D structural topology optimization (TO). This can be achieved by properly combining parallel computing and mesh adaption techniques by adopting a reaction–diffusion equation (RDE) based level-set method. Mesh adaptivity which discretizes and optimizes an implicitly defined surface (level-set interface) can allow us to reach an optimal solution with high-resolution and clear boundaries. Our framework can be easily extended to design real world engineering products which have complex geometries, and optimal designs can be directly manufactured out without post-processing phase. Furthermore, the proposed optimization algorithm can reach an identical optimal solution with different initial guesses. Our numerical implementation uses FreeFEM for finite element analysis (FEA), PETSc for distributed linear algebra and Mmg for mesh adaption. Several numerical examples and 3D printed prototypes support these remarkable features.
- FreeFEM supercharged: block solvers, parallel mesh adaptation, and more… / ○Jolivet Pierre (IRIT-ENSEEIHT, CNRS, France) [概要]
In this talk, I’ll present some recent advances with FreeFEM and its interface to the following parallel libraries: a) PETSc and HPDDM, which may now be used to solve (non)linear systems with multiple right-hand sides, e.g., tomography, b) SLEPc, and the recent interface to parallel singular value and nonlinear eigenvalue solvers, c) ParMmg, for mesh adaptation in parallel. Numerical examples will be provided throughout the talk, showing the flexibility and ease-of-use of the different new tools available in the latest versions of FreeFEM.
▷ [正会員OS] 時間遅れと数理(2) [9月10日:16:20-17:40:B]
- A prey-predator model with hunting cooperation / ○江夏 洋一 (東京理科大学) [概要]
本講演では,捕食項に現れる functional response が被食者と捕食者双方の個体数に依存するような,hunting cooperation を考慮した被食者-捕食者モデルの解の挙動を考える.maturation delay を考慮した場合の,時間遅れの長さが共存平衡点の分岐構造や解の漸近挙動に与える影響についても考察する.
- 時間遅れ項を伴うあるFokker-Planck方程式に現れるパルス解の周期運動の数理解析 / ○池田 幸太 (明大総合数理), Salort Delphine (Sorbonne Universite, laboratory LCQB) [概要]
ニューロンの膜電位の挙動を理解するために提唱されたLIF (leaky integrate-and-fire) モデルに対して導出されるFokker-Planck 方程式を取り扱う. このFokker-Planck 方程式には時間遅れが含まれ, その影響によりパルス型の空間形状を保ちながら時間周期に運動する特徴的な解が存在するが, ニューロンの集団としての時間周期的な発火現象と対応する. 本講演では抑制性ニューロン同士の結合強度を十分大きい場合を考え, この特徴的な解の性質を明らかにすることを目標とする.
- ある非線形遅延微分方程式系の星形周期解のフーリエスペクトル法を用いた近似解 / ○野澤 健三 (筑波大学), 高安 亮紀 (筑波大学) [概要]
ある非線形遅延微分方程式系の星形周期解について、フーリエスペクトル法を用いて、星型周期解の近似解を得た。本講演では、数値計算手法と得られた近似解の特徴について紹介する。対象となる非線形遅延微分方程式系は2つの遅延微分方程式を連立したもので、星形周期解の存在が予想されており、本数値計算結果は星型周期解の存在を示唆している。
- 離散系に対する遅延フィードバック制御~連続系の解析に向けて~ / ○宮崎 倫子 (静岡大学), Kim Dohan (Seoul National University), 申 正善 (静岡大学), 布藤 猛留 (静岡大学) [概要]
本研究は,遅延フィードバック制御が可能となる周期解の特性乗数の条件を導出することを目的としている.著者らは,限定的な条件下でその条件をすでに導出している.より一般的な条件へ拡張を考えるにあたり,離散システムに対する同様の条件を導出を考える中で,離散システムに対する条件を導きつつある.
本講演では,離散システムに関する結果を紹介するとともに,連続システムへの関連性についてその見通しを紹介する.
▷ [研究部会OS] 機械学習 [9月10日:16:20-17:40:C]
- スパースモデリングによるマテリアルズインフォマティクスと放射光データ解析への展開 【35分】 / ○五十嵐 康彦 (筑波大学システム情報系), 熊添 博之 (熊本大学産業ナノマテリアル研究所), 岩満 一功 (熊本大 学技術部), Fabio Iesari (九州シンクロトロン光研究センター), 瀬戸山 寛之 (九州シンクロトロン光研究センター), 岡島 敏浩 (あいちシンクロトロン光センター), 妹尾 与志木 (九州シンクロトロン光研究センター), 赤井 一郎 (熊本大学産業ナノマテリアル研究所), 岡田 真人 (東京大学大学院新領域創成科学研究科) [概要]
近年、材料科学への機械学習を展開することで効率的な材料設計を目標とするマテリアルズインフォマティクスが研究機関だけでなく、民間企業においても広がりをみせつつある。本講演ではその有効なアプローチの一つであるスパースモデリングを用いたマテリアルズ・インフォマティクスについて講演する。スパースモデリングとは、実データを説明する記述子は本質的に少ないことを事前情報として仮定することで、少ない情報から全体像を的確にあぶり出す機械学習の枠組みである。これにより、実験データを説明する有効な記述子抽出や計測データのノイズ除去への展開について述べる。
- 機械学習への情報幾何的アプローチ 【35分】 / ○杉山 麿人 (国立情報学研究所) [概要]
本講演では,ボルツマンマシンに代表されるGibbs分布の学習や,テンソル分解,信号源分離など,様々な機械学習タスクに対する情報幾何的アプローチを紹介する.双対平坦構造を持つ統計多様体に,隣接代数を利用して離散構造を取り入れることで,階層的な確率モデルを柔軟に設計することができる.さらに,モデル空間の体積に着目した汎化誤差解析についても紹介する.
▷ [一般講演] 一般講演(7) [9月10日:16:20-17:40:E]
- 非局所反応拡散方程式におけるフロント解同士の相互作用について / ○石井 宙志 (北海道大学大学院理学院), 栄 伸一郎 (北海道大学大学院理学研究院) [概要]
非局所項を持つ反応拡散方程式における線形安定な定常フロント解が複数配置された場合の,それぞれのフロント解の挙動について考える.
本講演では適切な積分核との合成積で表される非局所項を扱う.
フロント間の距離が十分離れているときには,距離に関する微分方程式を導出することで複数のフロント解の挙動が解析できることを説明する.
またいくつかの数理モデルに現れるフロント解同士の相互作用の解析結果を紹介する.
- 非対称単純排他過程における「分解予想」 / ○大橋 遼 (東京大学数理科学研究科博士課程) [概要]
十分大きなサイズの非対称単純排他過程について、ある局所的な状態が現れる確率は、より局所的な状態についての確率の積として分解できるという著しい性質が発見されている(分解予想)。本講演では、いくらかの具体的なモデルを取り上げながら、分解予想がどのような形であらわれるかについてご紹介したいと思います。
- ルジャンドル陪関数の変形と応用14 / ○田川 昭夫 (なし) [概要]
ルジャンドル陪関数Pn+m.mを変形すると、Rn.m(cosθ)*(sinθ)^mの形になる。液滴の内部流れ、e^ωtを因数に持つ減衰運動に応用する。ストークス近似式で解き境界条件は、表面でのθ、φ方向のせん断応力が0とする。解は、Rn.m*sinmφを含み、連続の式を満足するベクトルのヘルムホルツ解VA、VCと、ポテンシャル流の和となる。VC(r方向成分=0)を加算することで、任意のn.mでせん断応力=0とできる。
▷ [正会員OS] FreeFEM の開発と利用 [9月10日:17:50-19:10:A]
- FreeFEM 講習会 : 流体構造連成問題II — ALE法による強連成形式 【OS企画講習会】 / ○鈴木 厚 (大阪大学 サイバーメディアセンター) [概要]
Green St-Venant 非線形弾性体が Navier-Stokes 方程式で記述された流れから変形を受ける問題を考える. 固体と流体の境界での弾性体の速度場を調和拡張して得られる Piola 変換を用いることで流体に ALE 法を適用する. これにより変形した境界での速度場が一致し, また流体と弾性体の力が釣り合っている状態を, 変形前の参照領域で記述した単一の方程式系を得る. 弾性体は変位場と速度場の両方を未知とすることで, 系全体は一階の時間微分項のみを含むため後退 Euler 法を用いる. 変位場と速度場および流速と圧力に関する弱形式による非線形問題を FreeFEM により記述する方法を解説する.
▶︎ 広告
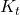 マトロイド予想 / ○谷川 眞一 (東京大学) [概要]
マトロイド予想 / ○谷川 眞一 (東京大学) [概要]